弾性衝突の節では保存則を用いて2体の衝突問題を調べた.
その際衝突後の質点の軌道が散乱角 に依存するという結果を得た.
しかしながらそこでの議論は衝突がどのような相互作用によって起こるのかなどの詳細に言及していない.
ここで2体間に中心力がはたらくとして衝突の詳細について考えていく.
片方の粒子はもう一方の粒子より十分重く運動は無視できるものとし,単に中心力場 を生み出しているものとして扱う.
このような固定された粒子を標的粒子,衝突してくる粒子を入射粒子という.
中心力場を介して相互作用する二粒子が「衝突」する場合,どれくらい近づいているかが重要となる.
このために2つの粒子がどのくらいの距離離れたところで相互作用し軌道が変化し飛び去っていくのかを記述しなければならない.
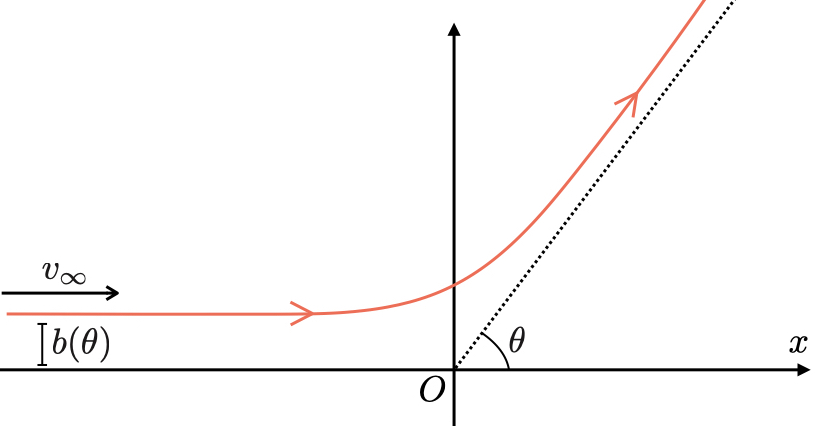
中心力場を感じない無限遠から標的粒子のある原点付近に向けて粒子を入射させる.
入射速度を とおく.
入射速度の向きと平行に 軸を設ける.
またこの 軸に垂直な
軸を設ける.
三次元空間だが,中心力場にせよ衝突問題にせよ考えるのはこの 平面で十分である.
軸と無限遠での入射粒子との距離を
とする.
は衝突パラメータと呼ばれる.
無限遠では相互作用を感じないので入射粒子のエネルギーは,
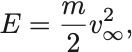
である.
ただし は入射粒子の質量.
入射後すぐに粒子は運動方程式,
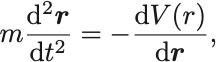
にしたがって運動する.
そうして再び無限遠方へ飛び去っていくが相互作用の影響で入射するときとは異なる方向へ向かうだろう.
そこで飛び去っていった無限遠での終端速度の方向と 軸(入射の方向)が成す角を散乱角
と定義しよう.
弾性衝突の節では入射速度と終端速度だけに注目していたことになる.
運動方程式は初期条件が与えられれば一意な解を持つので,初速 と衝突パラメータ
が同じであれば必ず同じ軌道を描き,同じ終端速度と散乱角を持つだろう.
したがって散乱角 は
と
に依存しているといえる.
関係式 を得ることが新たな問題として興ってくる.
次に散乱角 を実験で求まる量と結びつけたい.
実験ではサンプル数を増やすために1個の粒子ではなく,たくさんの粒子(光,中性子,ニュートリノなど)を含んだビームを入射させることが多い.
こうした実験では入射速度がそろったたくさんの粒子を用意して色々な方向に散乱される様子を観測する.
この実験での観測量は方位角(ここでの方位角は 軸と垂直な面へ散乱軌道を射影したときの角度である.散乱角同様,無限遠で測る)
,散乱角
における散乱粒子の個数
である.
複数の粒子を考える場合は散乱軌道は単一平面だけを考えることはできない.
しかしポテンシャルが球対称でかつビームが軸対称ならば散乱の軌道も軸対称になると予想できるので方位角 依存性は省略できる.
を調べることで散乱の角度分布が得られる.
そして入射速度をもつ1粒子に替えて,単位時間当たり単位面積を通過する粒子数 を定義する.
これは入射粒子流密度とか入射フラックスとよばれる.
無限遠での入射フラックス が原点付近にあるポテンシャル
と相互作用して角度
へ散乱される.
このとき角度 へ散乱される単位立体角あたりの粒子数を,
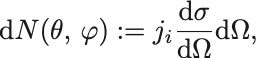
とおく. という量は単位時間当たりに,角度
にある微小面積
を通過する粒子数である.
それは入射フラックスに比例する(入射量が多ければ も多い)ので,
という量は入射フラックス依存性を除かれている.
を微分散乱断面積 (differential cross section) という.
微分散乱断面積は入射フラックスに依存せず,散乱によってどの方角に散乱されやすいかを表す量として粒子数よりも扱いやすい.
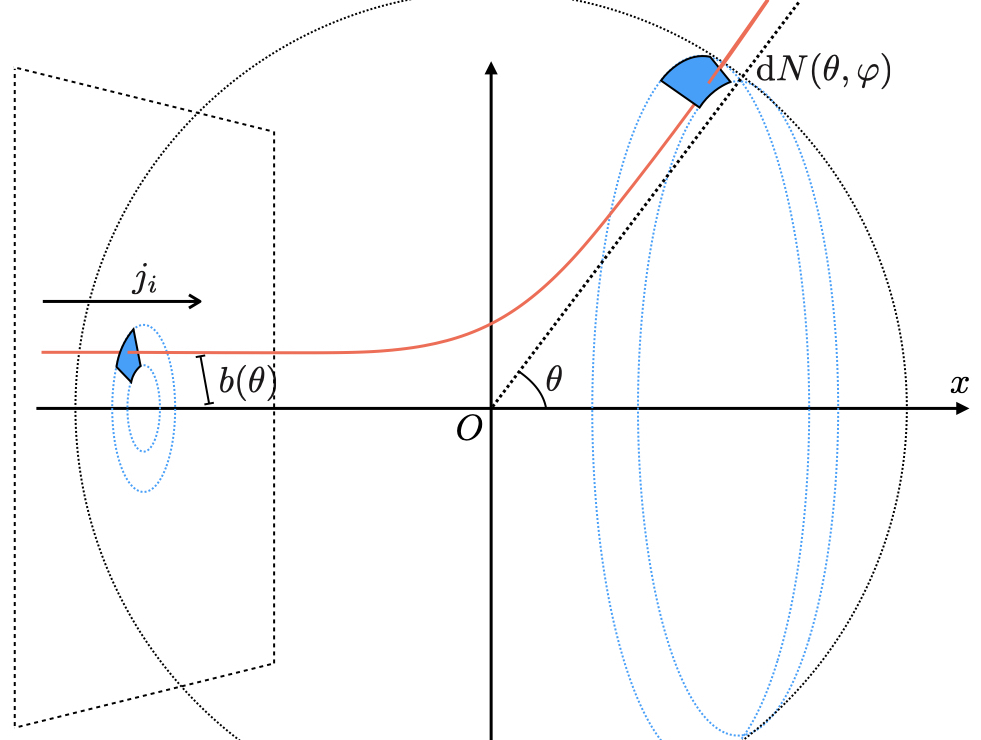
ところで散乱が軸対称である限り,散乱角 は初速度
と衝突パラメータ
が決まれば一意に決まる量である.
したがって入射フラックスに対しては,散乱角 に散乱される粒子の個数が衝突パラメータ
で入射する粒子の個数と一致していなければならない.
これはつまり半径 と
に囲まれたリングを通過して入射する粒子数
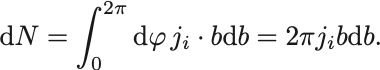
が,散乱角 と
に囲まれたリングを通過する粒子数に等しい.
ただし入射フラックスは軸対称性を仮定した.
以上の2式を比較すると,
微分散乱断面積と衝突パラメータの関係

が得られる.
ただし散乱断面積が正の値を持つように微分の絶対値をとっておく.
この式を用いれば衝突パラメータを を散乱角の函数として与えれば微分散乱断面積が求まることになる.
