二準位系 – 物理とはずがたり

Prerequisite

ここまで導入した道具の計算練習としてこの節では二準位系を扱おう．
というのも分配函数などの積分計算は統計力学の本質的な部分が見えにくいことがある．
シンプルな系で統計力学がどのような計算をしているかの流れを掴んでいく．
また後にスピンの系を扱うときに二準位系の計算が登場する．

二準位系とは質点ではなく，2つの状態しかとらないような抽象的な対象が $N$ 個集まった系である．
ふつうの質点は位置と運動量の（三次元では）6つの自由度があってそれぞれがエネルギー保存則を満たす範囲で連続な値を動き回ることができた．
二準位系では1つの自由度がとりうる状態は2つである．
それぞれに対応してエネルギーが

であるとしよう．
$a$ 番目のエネルギーが $\sigma_a\varepsilon$ とすると系のHamiltonianは

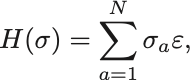
とかける．

まずミクロカノニカル分布を仮定して計算する．
ミクロカノニカル分布ではエネルギーが $E$ で固定されるので拘束条件として

が課せられる．
エネルギーが $+\varepsilon$ である対象の個数を $N_+$ ， $-\varepsilon$ の個数を $N_-$ とすれば，

を満たす．
よって $N_+=(N+E/\varepsilon)/2,\,N_-=(N-E/\varepsilon)/2$ である．
系がとりうる全状態数 $W$ は $N$ 個のうち $N_+$ が $+\varepsilon$ ，残りが $-\varepsilon$ をとる組み合わせであるから，

となる．
等重率の原理を仮定して系のエントロピーはBoltzmannの式 $S=k_{\mathrm{B}}\ln W$ とStirlingの公式から

を得る．
全エネルギー $E$ を内部エネルギー $U$ と同一視すれば系の温度は

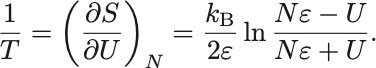
$U$ について解けば

となる．
ここで $\beta=(k_{\mathrm{B}}T)^{-1}$ ．

内部エネルギーが温度と粒子数の函数なので定積比熱は

となる．
これを二準位系のSchottky比熱という．
Schottky比熱の特徴としては低温極限 $T\to0$ と高温極限 $T\to\infty$ の両方で $C_{\mathrm{V}}\to0$ であり，その間の温度で1つの極大値をもつ．

ではSchottky比熱をカノニカル分布を用いて再導出しよう．
分配函数は

となる．
質点の場合は位相空間上の積分であったが二準位系の場合は2つの状態にわたる離散的な和である．
この和はあらわに書き下せて

となる．
これから直ちにHelmholtzの自由エネルギーが計算できて

内部エネルギーは

となりミクロカノニカル分布から計算したときと同じ結果を得る．

二準位系の温度の表式をもう一度よく見てみよう:

内部エネルギー $U$ は $-N\varepsilon$ から $N\varepsilon$ までの値をとりうる．
$U\to-N\varepsilon$ のとき， $\beta\to+\infty$ であり温度は $T\to +0$ である．
つまり系のエネルギーが最も低いとき温度は $0$ に近づく．
これは直感的にも正しい．

次にそこから徐々にエネルギーを増加させて負の側から $0$ へ近づける； $U\to-0$ ．
このとき $\beta\to+0$ で温度は $T\to+\infty$ となり発散する．．
さらにエネルギーを増大させると今度は $\beta$ は負の値をとり始め温度は $-\infty$ から増大を始める．
最終的に $U\to+N\varepsilon$ と最大値へ近づけると $\beta\to-\infty$ で温度は再び負の側から $0$ へ近づく．
つまり二準位系では正の温度より「高温」な負の温度 (negative temprature) が存在する．
しかしながら現実世界の安定な平衡状態において状態数が有限ということはあり得ず，温度が負になるということもない．