Prerequisite
座標系をもう少し扱いやすくするためにベクトルという概念を導入しよう.ベクトルは数学では代数学的に定義されるが力学の分野においては幾何的なイメージと対応づけて理解するのがよい.
3次元空間に導入された座標系の各点は測るべき3つの量をもっており と書いた.この物体の位置を表す数の組のことを数学的にはベクトル (vector) といい,組の中の数たち
をベクトルの成分 (component) という.とくに今の場合は点の位置を示しているのであるから,位置ベクトルという.
位置ベクトルは,物体が原点から測ってこの位置にあるということを,原点とその位置を結ぶ一つの矢印(矢は物体側にある)で表現する.位置ベクトルは物体がどの向きのどの距離にあるかを指定する.
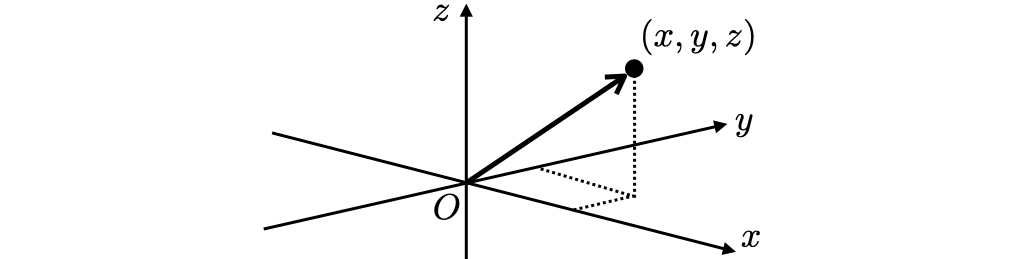
矢印の長さはすなわち原点からの距離であり,

で与えられる.
ベクトルは一般に次のような演算規則がある:
ベクトルの演算
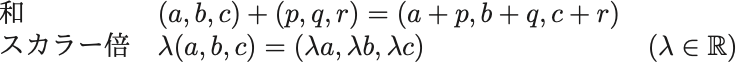
ここでスカラー (scalar) というのは(数の組ではない)ただの数のことでありベクトルと区別するときそうよぶ.
はじめ原点から という点へ移動したとする.次にその点を新しい原点として今度は
へ移動したとすると,その到達点ははじめの原点から測ると
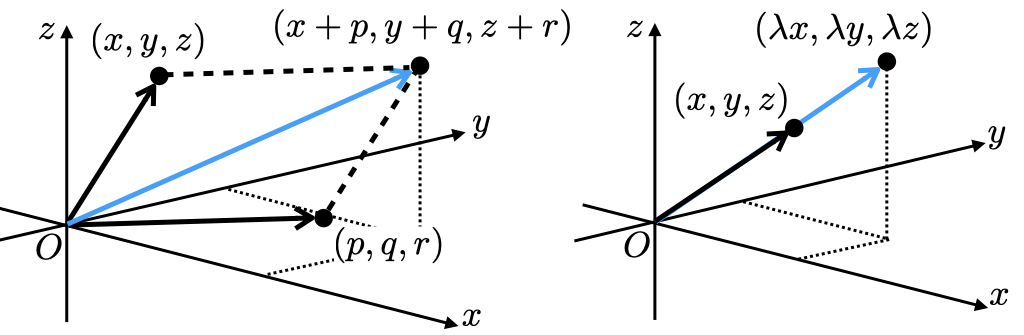
の位置となる.これが上式の位置ベクトルの和の意味である.足し算の性質から明らかに,

が成り立つ,つまりさっきの移動の順序を逆にしても到達する点は同じ位置ベクトルになる.幾何学的な対応では上式に現れるベクトルが描く図形は平行四辺形で,足したものはその平行四辺形の対角線になっていることがわかる.
ベクトルを数の組ではなく一文字で表すとき,普通アルファベットの太字や矢印が上についた文字を使い と表記する(本稿では太字を使う).この場合ベクトルの長さは
,あるいは単に
と書く.
また点 から点
へ向かうベクトルの場合は
と書く(向きと文字の順序をそろえる).物体の位置ベクトルは原点を
として
のように書く.このとき物体の存在する点
の座標は
である.
原点の位置ベクトルは である.すべての成分が
であるベクトルのことを零ベクトルといい,太字で
とかく.
よく採用されるベクトルの慣習表記を紹介しておこう.ベクトルの計算をするとき横に成分を並べるより縦に並べた方が見やすい.
そこで を,
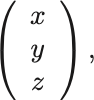
と書く.本稿でも式中では縦書きにする.
またベクトル の
番目の成分は
と表記することが多い.このとき
は数字
と思っても軸のラベル
と思っても良い.
成分 を並べたものとして
のように書くこともある.
空間に2点 をとる.2点の座標は位置ベクトルでそれぞれ,
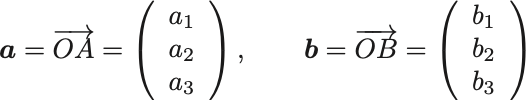
とする.このとき点 から見た点
の相対位置ベクトル
とは,
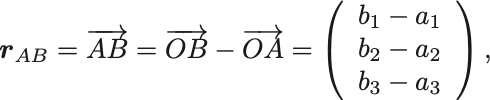
のことである. は,
を原点と見たときの
の位置ベクトルである.この計算によって別の観測者にとっての位置ベクトルを得ることができる.
観測者Aliceの座標の原点を ,観測者Bobにとっての座標の原点を
とする.
註:物理や数学(特に情報理論)では観測者をアルファベットA, B, Cに対応づけてAlice,Bob,Carolなどと名付けることがある.
このとき任意の点 の位置ベクトルに関して次が成立する,

これは異なる観測者間の位置ベクトルの変換式である.
次にベクトルどうしの積について見る.
ベクトルの足し算は普通の数と同じように定義されたがベクトルの掛け算は少し異なってくる.ベクトル に対して,
ベクトルの内積
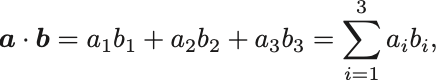
で定義される演算をベクトル と
の内積 (inner product) という.内積は2つのベクトルから一つのスカラーを与える演算である.
内積の定義から明らかに である.ベクトル
の始点と終点の距離はこのベクトルの大きさと一致しさらに
どうしの内積に一致する.したがって内積の定義は2点間の距離も定義している.
3つのベクトル があって
が成り立っているとしよう.ベクトルの大きさについて,
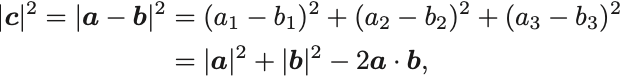
が成り立っていることがわかる.
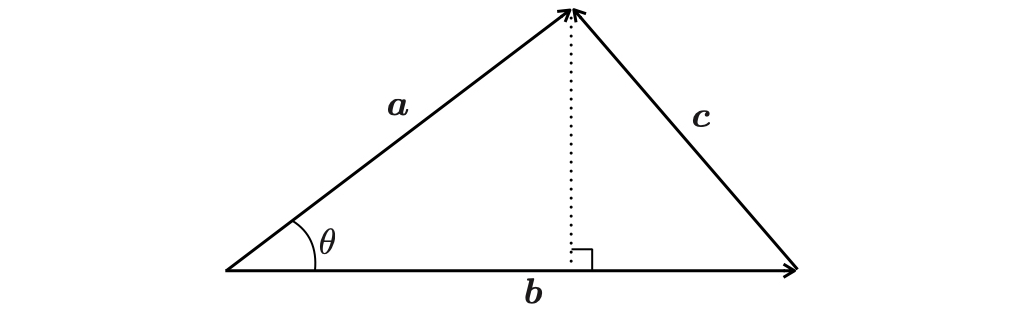
一方この3つのベクトルは三角形を形づくっているが,いまベクトル と
の間の角を
とおく.
図のように補助線をいれて三平方の定理から,
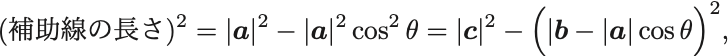
が成り立っている.ゆえに余弦定理とよばれる一般公式
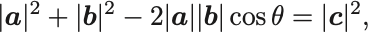
が得られる.これは三平方の定理の拡張である.
これとベクトルの大きさについての式を比べると,
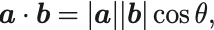
がわかる.これから2つのベクトルが与えられれば,その間の角度 はわかる.
とくに2つのベクトルが直交しているときは である.
ここでベクトルのスカラー倍について考えよう.
ベクトル とそのスカラー倍
の内積は

である.つまりベクトル と
のなす角の大きさは
または
であり,2つのベクトルは平行(または反平行)の関係にあることがわかる.
次に外積 (exterior product) とよばれる演算を定義する.2つのベクトル に対して,
ベクトルの外積
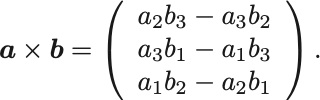
今度は2つのベクトルから1つのベクトルをかえす演算である.定義から であり演算の順序によって向きを反転させる.容易な計算から,

となって,ベクトルの外積はもとの2つのベクトルのどちらとも直交していることがわかる.
2つのベクトルが平行なとき, とかけて外積は,
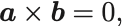
となる.
外積の大きさについてみてみよう.大きさの2乗はやや長い計算の後,

すなわち,

この表式から2つのベクトルの外積の大きさは( ならば)2つのベクトルの和が描く平行四辺形の面積になっていることがわかる.
ベクトルの内積に関しては次の有名な不等式を導くことができる:
Cauchy–Schwarzの不等式

この不等式はCauchy–Schwarzの不等式と呼ばれる.内積と角度 の関係式をみれば導出は容易で,
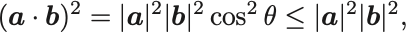
を得る.ここで であることを用いた.
ベクトル表記をやめて成分を直接かけば,
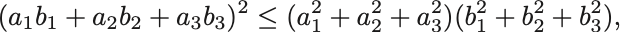
である.Cauchy–Schwarzの不等式は内積のもつ重要な性質の一つである.
上の導出では2つのベクトルの成す角度についての不等式から導いたが,本質的なことは内積の正定値性にある.正定値性とは,任意のベクトル の自分自身との内積
は必ず
以上であり,
に等しくなるのは
のときのみである,という性質のことである(問題参照).
Problems
ベクトル と
の内積と外積を計算せよ.
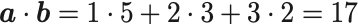
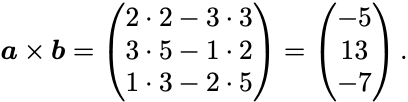
任意の実数 に対してベクトル
が正定値であることからCauchy–Schwarzの不等式を導け.
正定値性から自分自身との内積が 以上なので次の不等式が任意の
に対して成り立つ:
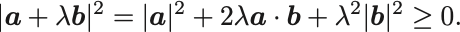
この不等式を についての2次不等式と思うと,不等式の意味は「左辺で表される放物線が
軸と2つ以上交点を持たない」ことと解釈できる.この条件は「(左辺)
の判別式が
以下」と等価である.
ゆえに判別式 について,

となる.これはまさにCauchy–Schwarzの不等式である.
Heronの公式: 三辺の長さが の三角形の面積が

で与えられることを示せ.ただし .
三角形の辺 のなす角を
とおくと面積は
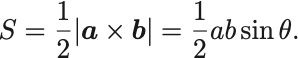
余弦定理より であるが,
についてとくと
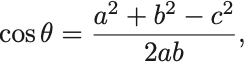
なので を消去できて
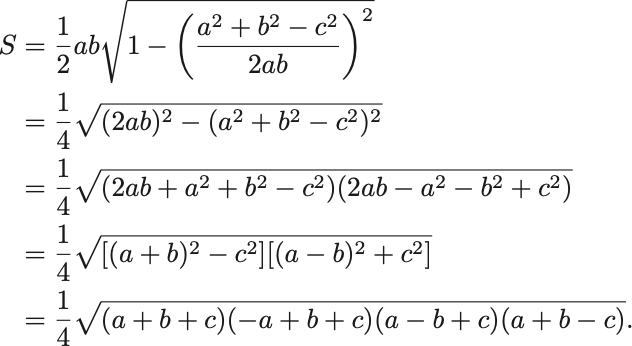
最後に とおけばHeronの公式を得る.
方向ベクトル: 任意のベクトル に対して,
と平行で大きさが
のベクトルが以下で与えられることを示せ:
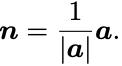
平行なのである実数 を用いて
とおける.
大きさが なので

ゆえに正の方を選べば がわかる.

“位置ベクトル” への2件のフィードバック