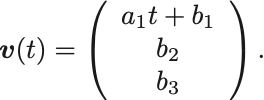微分を使って速さを定義しよう.
質点の軌道は時間の函数としての位置ベクトルであった.
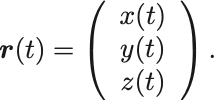
時刻 のときの位置ベクトル
と時刻
での
の差
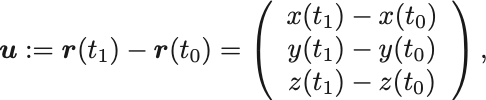
を変位ベクトル (displacement) という.
時刻 から
までの平均の速度ベクトルは
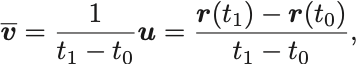
で計算される.これはベクトル量であるが各成分は平均の速さの定義に一致している. の極限をとって,

を定義する.これを質点の速度ベクトル (velocity) あるいは単に速度という.
この定義において極限操作は各成分でそれぞれ行われる.
たとえば速度ベクトルの 成分は微分
に等しく時刻
での位置の時間変化率を表す.
物理学においては時間による微分は 使って
などのように表すことが慣習となっている.
たとえば質点が直線軌道 の場合,微分の公式から
となり速度は一定となる.
速度ベクトルの大きさ,

は質点の速さ (speed) といい,速度と区別する.
たとえば速さ一定のまま曲線軌道を描く場合,質点の速度ベクトルは刻々と向きを変えていく.
速度ベクトルは位置ベクトルとは性質を異にするベクトルである.
速度 は定義からわかるように,物体の軌道上の位置ベクトル
で表される点を始点とするベクトルである.
また微分の性質から速度ベクトルは物体の軌道に接するような方向を向いている.
軌道の十分微小な区間ではほぼ直線とみなせて,微小な時間の間だけ物体がその方向に進んでいると解釈できる.

軌道が曲線の場合はこの見方は近似でしかないので物体は一般にはその速度ベクトルが指す点には進まない.

速度の微分においては必ず「質点の軌道に沿って」位置ベクトルを だけ微小変位させて定義することに注意しよう.
大きさは任意だが勝手な向きには微小変位をとることができない.
これを特に の方向微分という.
質点の軌道 から速度
を得るには微分計算で可能であった.
もし逆に速度 がわかっているときに軌道
はどうやって求めれば良いだろうか.
素朴には微分して となるような
を探せば良いが一般には難しい.
また微分の際定数項は全て となるので速度の情報だけからは原理的に求めることはできない.
微分の逆問題は「積分」とよばれる演算によって解かれる.
Problems
次の軌道の速度を計算せよ:
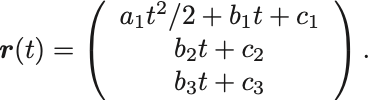
各成分ごとに微分を計算する.
まず 成分は
.
成分は
と求まる.
したがって速度ベクトルは