Prerequisite
この節では極限と微分の両方を使った数学的道具を紹介する.
まず最初に次の定理を事実として認めよう:
有界性定理
が区間
上で上に有界
ある実数
と
が存在して任意の
において
.
と
は区間
内に存在するとは限らない.これは有界性定理として知られる.
この定理を強めた,
最大・最小値の定理
が区間
上で上に有界
は
上で最大値と最小値を有する ,
も成立する.
有界性定理を利用して証明しよう.
有界性定理と実数の連続性より任意の と集合
に対して,

を満たす上限 が存在する.
今, となるような
が
上には存在しないと仮定しよう.
よって常に であり,
が
に等しくなることはない.
の連続性より,
を定義すると
は
上で連続である.
有界性定理より は有界である.
一方で の最小性から任意の
に対しある
が存在して,

すなわち

であり は有界ではない.
したがって に矛盾が生じるので,背理法により
となるような
は
上に存在しなければならない.
よって は
上に最大値
を有する.
に対して同様の議論を適用することで
が最小値を有することもしたがう
.
1つ注意が必要なことは開区間では成り立たないことである.
たとえば函数 は開区間
上に最大値も最小値も持たない.

最大値,最小値を取る点においては函数の微分の値が となることが示せる.
Rolleの定理
函数 が
上で連続かつ
上で微分可能とする.
さらに であるとき,

Rolleの定理は両端が等しい区間のどこかで必ず微分が となる点が存在することを主張する.
まず が定数函数の場合は任意の点で成立する.
がそれ以外の場合,最大・最小値の定理より(異なる値の)最大値と最小値を区間内にもつ.
で最大値
をとる.
ならば
.
においては,

を満たし極限 をとれば左辺は微分の定義より

同様にして においては,

を満たし極限 をとれば左辺は微分の定義より

となる.
以上のことから でなければならない.
ではない場合(つまり両端の点で最大値をとる場合),最小値となる点
を考えて同様の議論をすれば
が導かれる
.
両端の値が等しくない の場合にも定理を拡張できる.
Cauchyの平均値の定理
2つ函数 は区間
上で連続かつ
上で微分可能とする.
また任意の で
とする.
このとき,
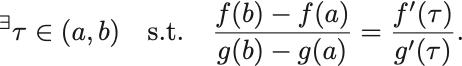
証明のために函数

を定義すると, も
上で連続かつ
上で微分可能,さらに
を満たす.
したがってRolleの定理により

これはとりも直さず


Cauchyの平均値の定理の特別な場合として の場合は
が
上で連続かつ
上で微分可能ならば

が成立する.
こちらはLagrangeの平均値の定理として知られ,両端を結んでできる直線と平行となるような の接線が区間内に存在することを主張する.
また とすればRolleの定理がしたがう.
最後に不定形 (indeterminate form) の極限について議論しよう.
不定形とは のとき,あるいは
かつ
のときの極限

のことである.
要するに極限での函数値が や
のような形のことを指す.
不定形はそのままでは収束性を判断することはできない.
不定形の極限については次のl’Hospitalの定理が有用である:
l’Hospitalの定理
で微分可能な函数
に対し,
かつ
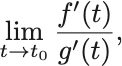
の極限値が存在するとき
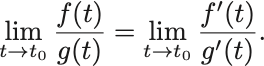
大雑把に証明しておくと,

と変形して, においてはCauchyの平均値の定理により

においても同様の式が成立.
とすると
なので

となり示された .
は
に置き換えてもl’Hospitalの定理は同様に成り立つ.
とすると

右辺にl’Hospitalの定理を適用して

したがって

l’Hospitalの定理はさらに かつ
の場合にも拡張できる(証明は省略する).
この場合も は
に置き換えても良い.
例として の
の極限を求めよう.
これは の不定形であるがl’Hospitalの定理により

とわかる.
l’Hospitalの定理を1回適用しただけではわからない場合でも複数回適用することで極限値を求められる場合もある.
函数 の
の極限は
の不定形である.
l’Hospitalの定理により

となって依然 の不定形だが,もう一度l’Hospitalの定理を適用すれば

がわかる.
指数函数は何回微分しても のままだが多項式は有限回の微分で定数函数となる.
したがって任意の正整数 に対し

となる.これは指数函数の増大のスピードが多項式函数より遥かに速いことを意味している.
このようにl’Hospitalの定理は2つの函数の収束の速さを比較するのに用いることもできる.

“微分と極限” への1件のフィードバック