弧度法では半径 の円周を切り取る長さによって角度を定義する.
この考え方を拡張すれば三次元における「角度」を定義できる.

半径 の球面を考える.
任意の底面をもつ錐体を考えて,この頂点と球面の中心が重なるようにしたとき,球面と錐体の交わる部分の面積で立体角 (solid angle) を定義する.
立体角は無次元量であり単位はステラジアン を用いる.
球面の表面積は であるから全立体角は
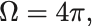
である.

立体角の計算をするためにも区分求積法を用いる.
球面を経線と緯線で区切って小さな(球面に沿った)長方形に分割する.
この長方形の経線方向の長さは であり,緯線方向の長さは
である.
したがって微小な長方形の面積は

で与えられる.
任意の錐体の立体角はこれらの総和でかける.
特に もわかる.
立体角は球面極座標で動径座標 を
で固定した座標とも言える.

任意の有界な曲面 の立体角
は,

によって計算できる. は微小面要素の位置ベクトル.
は球面の法線ベクトル(大きさが
で曲面に直交する向きを持つベクトル)であり,
は曲面の法線ベクトル,
は曲面の微小面要素である.
は曲面
上の微小面要素からその面を通る球面への射影である.
はこの球面と半径
の球面との相似比である.
球面極座標の函数 について

とおく.
このとき物理量 は物理量
の単位立体角あたりの値を表すことになる.
そこで記号として

と書く.
また微小立体角の面要素を と略記して
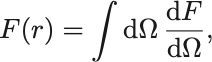
と書くこともある.
物理量 が軸対称の場合は
軸をこの対称軸となるようにとれば
に依存しないようにできる;
.
このとき 積分は
を与えるから

一方で単位角あたりの量として

と表すと2つの微係数について

が成立する.
