振動の二体問題

Prerequisite

単振動

質点がバネなどでつながれて互いに影響を及ぼし合いながら振動することを連成振動(coupled vibration)という．
ここでは質点が2つの場合に限り，その簡単な例を取り上げる．

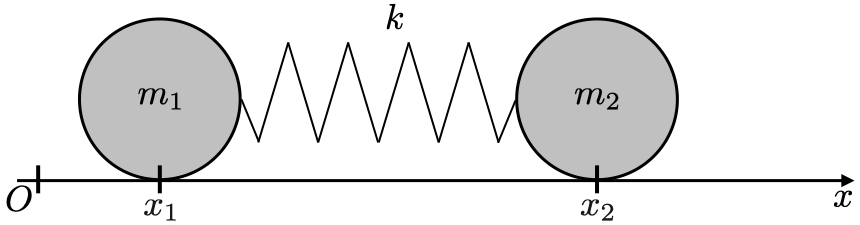
1つ目の例では2つの質点（質量 $m_1,\,m_2$ ）がバネ定数 $k$ ，自然長 $l$ のバネで繋がれているとする．
この2質点を少し引っ張って静かに放すと振動し始める．適当なところに原点をとりバネに沿って $x$ 軸を用意する．
ある時刻での質点の位置は $x_1,\,x_2$ （ $x_1<x_2$ ）とし，そのときのバネの伸びを $\xi=x_2-x_1-l$ と書こう．
質点に働く力はそれぞれ $k\xi$ と $-k\xi$ である．
それゆえ質点の運動方程式は，

となる．形に注目すると右辺は相対座標 $x_{\mathrm{rel}}=x_2-x_1$ にのみ依存する．
したがって二体問題の議論を適用することができる．
つまり運動方程式は相対座標 $x_{\mathrm{rel}}$ と重心座標 $x_G=(m_1x_1+m_2x_2)/M$ （ $M=m_1+m_2$ は全質量）に分解できる．
運動方程式の和をとると $M\ddot{x}_G=0$ となり，重心座標が等速直線運動することがわかる．

運動方程式の2つ目に $m_1$ をかけ，1つ目に $m_2$ をかけたものの差をとると $\mu \ddot{x}_{\mathrm{rel}} =-k(x_{\mathrm{rel}}-l)$ となる．
ここで $\mu=m_1m_2/(m_1+m_2)$ は換算質量．
$\xi:=x_{\mathrm{rel}}-l$ とおけば $\ddot{\xi}=-\omega^2\xi$ という単振動の運動方程式に帰着する．
ここで $\omega=\sqrt{k/\mu}$ とおいた．

単振動の一般解は $\xi=c_1\cos\omega t+c_2\sin\omega t$ ．
初期条件を $x_G(0)=0,\,\xi(0)=A$ ， $\dot{x}_1(0)=\dot{x}_2(0)=v_0$ とおけば $c_1=A,\,c_2=0$ となって，

と定まる．元の質点の座標の解は，

第1項は並進運動を表し，第2項は重心座標からの距離が単振動することを示している．

2つ目の例は箱の中に2つの質点（質量 $m_1,\,m_2$ ）が3つのバネで繋がれている状況を考える．
3つのバネのバネ定数を $k_1,\,k_2,\,k_3$ とする．
各質点がそれぞれ平衡点（自然長の位置とは限らない）から $x_1,\,x_2$ だけずれているとき，質点に働く力を求める．
たとえばバネの自然長を $l_1,\,l_2,\,l_3$ とし $l_1+l_2+l_3<L$ であるならば力がつり合っているときはバネは全て伸びていなければならない（ $l_1+l_2+l_3>L$ の場合は「縮み」に読み換える）．
平衡点で働いている力は相殺するので考えなくて良い．
したがって質点の平衡点からのずれをそれぞれ $x_1,\,x_2$ とするとき質点に働く正味の力は $-k_1x_1+k_2(x_2-x_1)$ となる．
同様に質点2に働く正味の力は $-k_2(x_2-x_1)-k_3x_2$ となる．

運動方程式は，

となる．このままでも方程式を解くことはできるが，簡単のため $m_1=m_2$ とし，3つのバネも全て同じもの $k_1=k_2=k_3=k$ としよう：

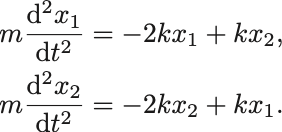
1つ目の例と同じように二体問題の解法に従って2質点の重心座標と相対座標についての運動方程式に書き換える．
2式の和から

よって質量 $M=2m$ の重心座標 $x_G=(x_1+x_2)/2$ はバネ定数 $2k$ で単振動する．
他方で2式の差からは

となって質量 $\mu=m$ の相対座標 $x_{\mathrm{rel}}$ はバネ定数 $3k$ で単振動する．

$\omega_1=\sqrt{k/m},\,\omega_2=\sqrt{3k/m}$ とおくと，得られた2つの方程式は一体の振動の問題だからただちに一般解を

と与えられる．
これらからそれぞれの質点の軌道が

と求まる．

書き換えた2組の方程式は重心座標と相対座標についての方程式と解釈できるが，この点について考察を加えよう．
和 $x_1+x_2$ の振動は2質点を質量 $2m$ の1つの質点とみなすような運動方程式である．
そのため中央のバネが無視され有効的にバネ定数は $2k$ となる．
もし初期条件として $x_1$ と $x_2$ を同じ方向へ同じ距離ずらす場合， $A_2=0$ となり相対座標の運動は消えて重心座標の振動だけになる．
よってこの場合2質点は同じ振幅と周期となり振動の向きも同じとなる．
このような振動の仕方を同位相という．

他方で差 $x_2-x_1$ は相対座標についてなので全てのバネが寄与してくる．
初期条件として $x_1$ と $x_2$ を逆の方向へ同じ距離ずらす場合， $A_1=0$ となり重心座標の運動は消えて相対座標の振動だけになる．
2質点は振幅や周期は同じだが振動の向きが逆になる．
このような振動の仕方を逆位相という．

振動論の解はこのような振動の仕方の線型結合で表される．
これを重ね合わせの原理という．
重ね合わせの原理はもとの微分方程式が変数 $x$ について線型であることに由来し，そのような運動方程式を持つすべての物理学において有効な原理である．
たとえば（真空中の）電磁気学におけるMaxwell方程式，量子力学におけるSchrödinger方程式など．

次節ではこれら線型結合の解をシステマティックに導く数学的道具，線型代数学を紹介する．
この方法は二体問題に限らず $N$ 体の問題へ一般化され，さらには無限次元にも拡張可能である．
無限次元の振動論については電磁気学の章で議論する．