Prerequisite
この節では力学の系に対して確率論を導入していく.
まず確率を導入するために標本空間を定めなければならない.
すなわち系がとりうる状態の集合を定義したい.
正準形式の力学の系では状態は位相空間上の点 で指定される.
理論上,位相空間上の軌道は正準方程式と初期条件によって完全に定められる.
しかし統計力学で扱う多粒子の系ではそれは実際には不可能である.
位相空間上の軌道はたとえばエネルギー保存則などの拘束条件によって制限がかかる.
孤立系に対してはエネルギーが保存するので系のHamiltonianを とすると,位相空間の軌道は
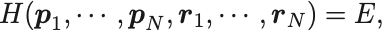
の表す超曲面上に限られる.
座標も運動量も有界とするとこの超曲面は閉曲面である.
この閉超曲面が囲む領域を とし,閉超曲面を
とおく.
そこで標本空間として に選ぶという手がある.
この選び方は厳密ではなく,実際の軌道がどのような状態を取りうるかはわからないが少なくともエネルギーが保存する領域内にあるはずだとして広めの領域にとっている.
このような選び方をしてもよいというのは1つの仮定である.
しかしながらわれわれが興味があるのは系のマクロな熱力学的性質の導出であって,個々の状態の確率分布ではないことは重要である.
この標本空間の選択における仮定について理解するために,熱力学における平衡状態について考えよう.
熱力学第〇法則より,任意の孤立系は十分時間が経つとマクロな熱力学変数が一定となる熱平衡状態へ緩和する.
このとき初期条件によって緩和する先の平衡状態はミクロにみると様々に異なる可能性がある.
しかしマクロに見て温度などの熱力学変数を観測したときそれらは同一の値を与えると考えられる.
そこで仮定として
熱平衡状態の典型性
位相空間内の取りうる状態のほとんど全てが同一の熱平衡状態に対応する
としよう.
「ほとんど」と断ったのは,1つの粒子だけ運動し残りは静止している状態など,明らかに熱平衡状態ではない状態は存在するからである.
しかしそのような状態は無視できるくらい少ない(測度 ).
この仮定を熱平衡状態の典型性 (typicality) という.
典型性の仮定により系の標本空間を位相空間の取りうる状態全てにとっても,そして実際にはそのうちの限られた領域に軌道はとどまっているとしても,問題なく熱平衡状態を議論できる.
エネルギー保存則などで制限された位相空間の部分集合としての標本空間 が得られたとしよう.
に対して確率密度函数
は規格化条件
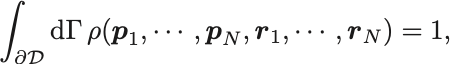
を満たす.
ここで位相空間測度
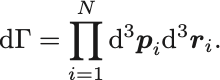
統計力学ではミクロな理論から出発するため量子論からの結果を持ち出さなければならない点が2つある.
1つ目は粒子の不可弁別性で,量子論的には粒子を区別することが原理的に不可能である.
そのため粒子のラベルで区別した足し上げをすると量子論的には重複してしまう.
そこで で割っておいて重複をキャンセルしておく必要がある.
2つ目は座標と運動量に関する不確定性原理である.
座標と運動量の測定精度の積はPlanck定数 以下にすることができない.
つまりこの体積 以下の位相空間の領域に関しては状態を原理的に区別できないことになる(より正確には,有界ないわゆる束縛状態では量子化されるためその間の連続な状態が存在しない).
そこでこの定数でも割っておく必要がある.
以上2点については事実として認めることにして量子論と整合する規格化条件を
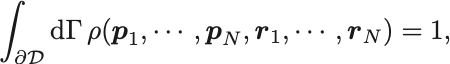
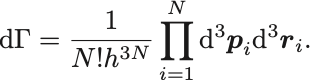
とする. は角運動量の次元を持っているのでちょうど位相空間測度は無次元化される.
ではこの確率密度函数と熱力学を結び付けよう.
特に確率密度函数とエントロピーが結び付けば,熱力学の諸法則によって系の平衡状態は記述できる(熱力学の第〇法則と第二法則の導出は未解決問題である).
そのためにはさらに3つの仮定が必要となる.
1. エントロピーは確率密度のみの函数 の期待値である:
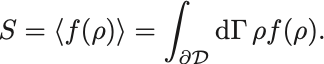
2. エントロピーは相加変数である:部分系 と
に対して
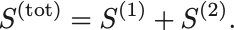
3. 部分系 と
の確率密度は統計的に独立である:
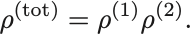
仮定2は熱力学からの要請だから統計力学での仮定は1と3である.
仮定2を期待値で書けば
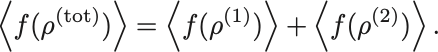
左辺については仮定3を適用して
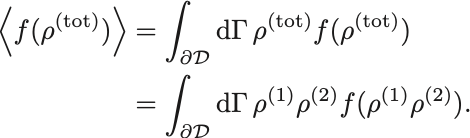
右辺については規格化条件 を挟み込んで
なので
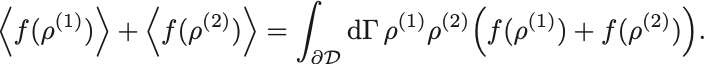
任意の確率密度で成立するためには
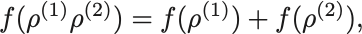
が成り立たなければならない.
これを満たす函数は
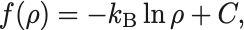
である.
ここで はBoltzmann定数であり実験から決められる値である.
は定数でエントロピーの基準点に依存している.
古典的には問題にならないが,熱力学第三法則によれば であるのでここでもそうしておく.
詳しくは量統計力学の章で議論する.
結局
Gibbsエントロピー

によってエントロピーが計算できることがわかった.
このような統計力学的なエントロピーをGibbsエントロピーという.
エントロピーの計算方法がわかったのであとは確率密度を定める問題が残っている.
確率密度は系の設定に応じていくつかの形が知られている.
次節から代表的なものについて求めていくことにしよう.
Problems
次を満たす連続函数 を求めよ:
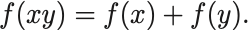
条件式の両辺を で微分すれば
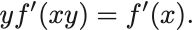
ここで とおけば
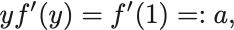
となるので積分して
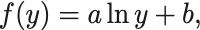
を得る. は定数.
初学者なので誤っていたらすみません。
「3つの仮定」で確率変数の独立性を仮定しているので、この確率変数は粒子を区別していると思います。したがって、規格化条件でN!h^3Nで割る必要はないと思います。
また、dΓ=1/(N!…と置いてしまうと途中で使うdΓ=dΓ1*dΓ2が成り立たなくなってしまうと思います。
dΓの定義を最初のまま(N!を含まない定義)にしてボルツマンの定理を証明した後、次のミクロカノニカル分布のページでは
p=1/Wではなくp=1/(N!*h^n*W) (https://en.wikipedia.org/wiki/Microcanonical_ensemble#Classical_mechanical) としたほうが良いのではないでしょうか?
いいねいいね