エントロピー

Prerequisite

Clausiusの不等式

前節で任意のサイクル $D$ に対するClausiusの不等式による熱力学第二法則の表現を得た：

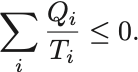
この不等式の等号成立は $D$ が可逆サイクルであることであった．
等号が成立している場合に，サイクル $D$ の途中の2つの平衡状態 $\mathcal{A}$ と $\mathcal{B}$ に注目しよう．
$\mathcal{A}$ と $\mathcal{B}$ はサイクル $D$ を使って移りあえる．
そこで2つの可逆過程 $\gamma_1:\mathcal{A}\leftrightarrow\mathcal{B}$ と $\gamma_2:\mathcal{A}\leftrightarrow\mathcal{B}$ を考え，可逆サイクル $D$ は過程 $\gamma_1$ と $\overline{\gamma}_2$ で構成されるとする．
そしてClausiusの不等式の和を $\gamma_1$ におけるものと $\overline{\gamma}_2$ におけるものとに分離する，

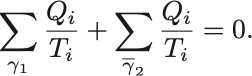
定義より $\overline{\gamma}_2$ に沿ってやり取りされる熱 $Q_i$ は $\gamma_2$ に沿った $-Q_i$ に等しいので，

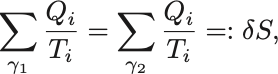
が成り立つ．
つまり可逆過程 $\gamma_1$ に沿って $Q_i/T_i$ を足し上げたものと $\gamma_2$ に沿って足し上げたものは等しいことを意味する．
ここで総和 $\delta S:=\sum_iQ_i/T_i$ は始点と終点の平衡状態のみに依存し，その間の過程のとりかたに依存しないことに注目しよう．
これは熱力学第一法則における内部エネルギーの変化 $\delta U$ と類似した量と言える．

次にサイクル $D'$ が不可逆過程 $\Gamma:\mathcal{A}\rightrightarrows\mathcal{B}$ と可逆過程 $\overline{\gamma}_1:\mathcal{B}\leftrightarrow\mathcal{A}$ とで構成されるとする．
$D'$ は不可逆サイクルなのでClausiusの不等式の等号は成り立たず，

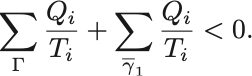
定義より $\overline{\gamma}_1$ に沿ってやり取りされる熱 $Q_i$ は $\gamma_1$ に沿った $-Q_i$ に等しく，可逆過程の詳細によらず $\delta S$ に等しい．
それゆえ

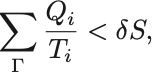
という不等式が不可逆過程 $\Gamma$ に関して成り立つ．
すなわち不可逆過程 $\Gamma$ に沿って $Q_i/T_i$ を足し上げたものは必ず可逆過程のときの値 $\delta S$ より小さい．

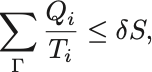
こうして任意の過程 $\Gamma:\mathcal{A}\rightarrow\mathcal{B}$ に対して

が成立し，等号が成立するのは $\Gamma$ が可逆過程のときである．
Clausiusの不等式がサイクルの間の熱のやり取りに注目していたのに対し，こちらは過程の間の熱のやり取りに注目している．

次に準静的過程 $\gamma:\mathcal{A}\overset{\mathrm{q}}{\leftrightarrow}\mathcal{B}$ を考える．
たとえば準静的に温度を $T$ から $T+\delta T$ まで上昇させる過程を実現したいときには温度を十分ゆっくり上げる必要がある．
この過程を実現するためには $N$ 個の熱浴を用意し， $i$ 番目の温度を $T_i=T+i\delta T/N$ に制御する．
そして1つ目から順番に系に接触させ熱 $Q_i$ をわたしその温度を $i\delta T/N$ ずつ上げていく．
$N$ を十分大きくすれば温度の上がり方は緩やかになり準静的とみなせ， $N\to\infty$ の極限では連続な温度変化の過程と見做すことができる．
微小温度変化 $\mathrm{d} T$ の間にやりとりする熱を $d'Q$ とすると和を積分に置き換えることができて，

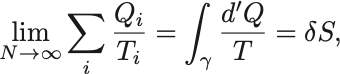
と書ける．
ただし熱は過程に依存する量であり，微小過程の両端での変化量とは異なることを明示するために $\mathrm{d}$ は用いず $d'$ を使っている．
ところで $\delta S$ という量は経路に依存しないので $d'Q/T$ には「ポテンシャル」が存在し，

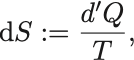
とおける．
これは可積分条件に他ならず原始函数を $S$ として，

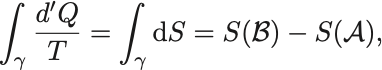
が成り立つ．
よって $\delta S=S(\mathcal{B})-S(\mathcal{A})$ である．
この「ポテンシャル」 $S$ をエントロピー (entropy) という．
エントロピーの基準を適当な平衡状態 $O^*$ における値 $S(\mathcal{O}^*)$ に選ぶことで，任意の平衡状態でのエントロピーの値を定められる．

エントロピーは熱力学において最も特徴的な役割を果たす．
また力学には対応する量が存在しない．
この節では準静的過程でやりとりされる熱をエントロピーの始点と終点の値と結び付けられることを見た．
しかしエントロピー自体は各平衡状態で定義することができるのでもっと一般的な関係式を得ることができる．
エントロピーの性質を次節で詳細に議論しよう．