Prerequisite
この章ではもう一つの力学の形式である正準形式 (canonical formalism) あるいはHamilton形式と呼ばれる理論を見ていく.
正準形式はLagrange形式より見た目も数学的にも美しくまとめられる.
統計力学や量子力学は正準形式を出発点にする.
まずLagrange形式から出発して正準形式の基礎方程式を導いてみよう.
一般にLagrangianは位置,速度と時間の函数であった.
Lagrangianの全微分をとってみると,
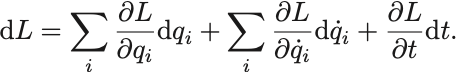
がEuler–Lagrange方程式を満たすとすると,
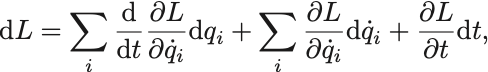
となる.(保存するかどうかは別として)一般化運動量の定義は,
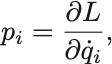
であったから,
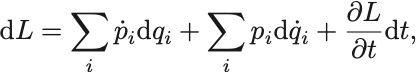
と書き換えられる.ただし が
の函数であることに注意せよ.
運動量の定義式は について解けると仮定して,
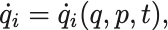
が得られたとしよう.そして次のような函数を定義しよう:
Hamiltonian
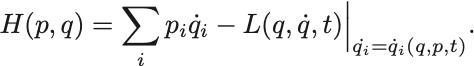
右下は, を代入して
の定義式に
が陽に現れないようにした,ということを示す.
今度は の全微分をとってみると,
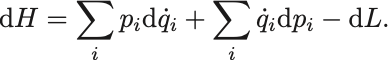
の式を代入すれば結局,
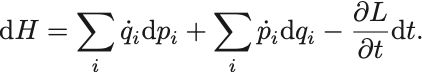
これより という量は位置とそれに対応する運動量の函数
になっている.
を系のHamiltonianという.
またここで行った独立変数の取り替えを一般にはLegendre変換という.Lagrangianの独立変数は位置と速度であったものがLegendre変換によってHamiltonianでは位置と運動量に置き換わっているのである.Legendre変換については次の節で詳細を述べる.
Hamiltonianの全微分は,
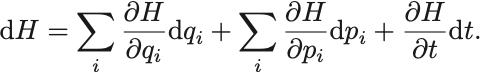
時間を固定して二式を比較してみれば次の 個の方程式が得られる:
正準方程式
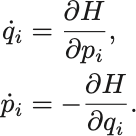
これらを正準方程式 (canonical equations) あるいはHamilton方程式という.
この方程式は位置と運動量について非常に対称性が良い.そういう意味で正準という.また の組を正準変数といい正準形式での基本変数として扱う.
一般のポテンシャル の系のLagrangian
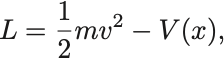
から正準方程式を導いてみよう.運動量は なので

これから導かれるHamilton方程式は,
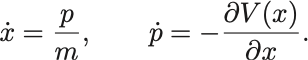
第1の式から であり,これを第2の式に代入すれば,
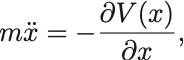
となってNewton方程式を再び得る.
以上のことは次元を増やしても同様に成り立つ.たとえば3次元の 個の質点のLagrangianに対応したHamiltonianは,まず直交座標では
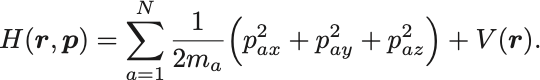
ただし .
円筒座標では,

ただし .
最後に球面極座標では,
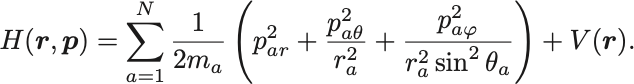
ただし .
Problem
1次元の調和振動子の系のLagrangian,
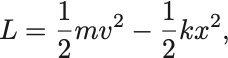
からHamiltonianを求め,正準方程式を導出せよ.
運動量は .定義より,
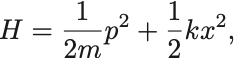
となる.よって正準方程式は,

