Prerequisite
離散的な値をとる確率変数の議論を連続的な確率変数 に拡張しよう.
連続な場合,標本空間に含まれる事象の数(濃度)は連続無限である.
それゆえに各事象の総和をとったときに発散してしまい を満たせなくなる.
またデータ数をどれだけ増やしてもたかだか可算なので全ての事象の統計的確率は求められない(ほとんど全ての事象に対して確率が になる).
しかしながら標本空間を有限個の領域 に分けて連続な確率変数
のとる値がある領域
に入る確率
は定められる.
簡単のため標本空間を実数 とする.
確率変数 がある実数
以下である確率を
とおく.
確率変数 が区間
に入る確率は
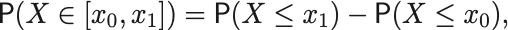
で計算できる.
この形を見て がある函数
の原始函数になっているとみて
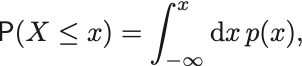
と書き換える. が
の単調非減少函数であることから

である.
また なので
確率密度関数の規格化条件

を満たす.
この を確率密度函数といい,この積分条件を規格化条件 (normalization condition) という
統計力学で登場するのはこの確率密度函数である.
が区間
に入る確率は,
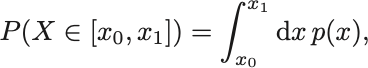
で求められる.
積分変数を によって変換すると全確率は,
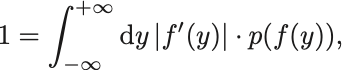
となるので変数 でみたときの確率密度は
でありJacobianが付くことに注意する.
2つの確率変数 については離散的な場合と類似の関係式,
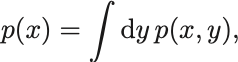
が成り立つ.
また条件付き確率,
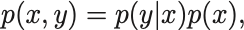
が定義される. が2つの確率変数
について
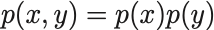
となるとき と
は統計的独立という.
期待値と分散も離散的な場合と同様に
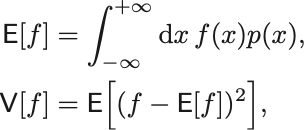
で定義する.
離散的な場合と同様に期待値の計算は線型である:2つの函数 と実数
に対し
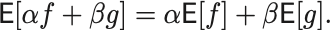
多変数 の場合には共分散を
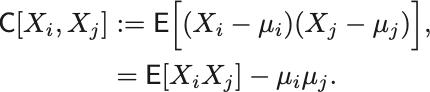
と定義できる.
ここで は平均.
統計学,物理学において最も重要な確率密度函数であるGauss分布,または正規分布 (normal distribution) :
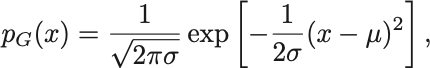
を例にあげよう.
ここで は正の定数.
まず平均は
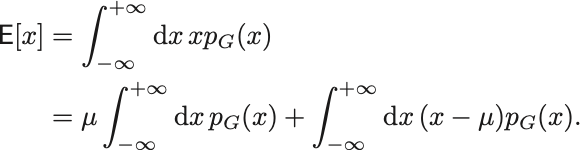
第1項は規格化条件より に等しく,第2項は被積分函数が奇函数なので
である.
よって .
次に分散はGauss積分の公式
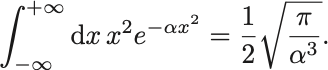
を用いて定義から計算すると,

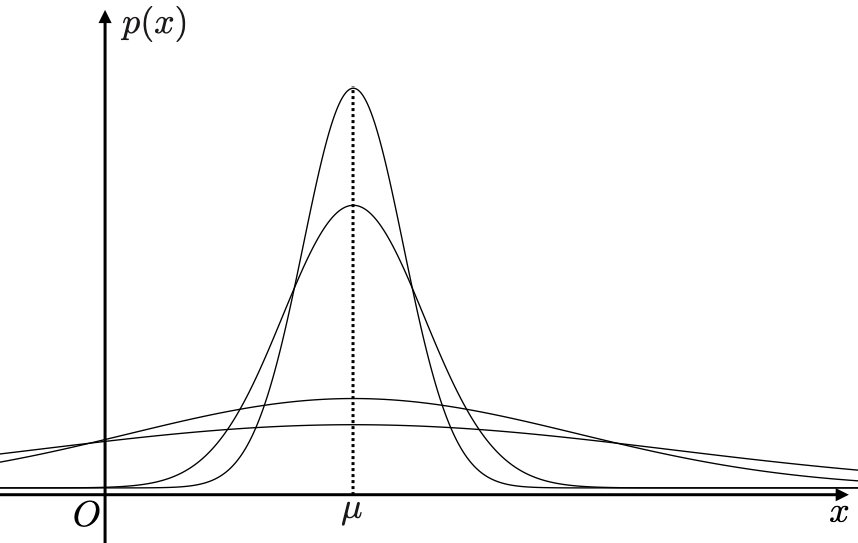
Gauss分布の2つのパラメータ について補足しおく.
Gauss分布は山型のピークをもったグラフとなる. はそのピークの位置に等しくグラフの並進移動を制御する.
ピークの幅はおよそ に等しく,ピークの高さは
である.
したがって が小さいととピークは高く鋭くなり,大きいとピークは低くなだらかになる.
これは全確率が に等しいことを保つためである.
Problems
多変数Gauss分布:以下の多変数 に対する確率密度函数の平均,共分散を求めよ

ただし は定ベクトル,
は対称かつ正定値(固有値が全て正)な行列.
まず平均は,

第1項は被積分函数が奇函数なので ,第2項は規格化条件により
に等しい.
よって .
次に共分散は定義より,
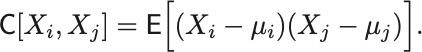
期待値の定義より,
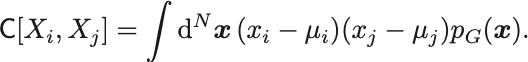
Gauss積分を計算するためには一度 を対角化するような変数
へ移る必要がある.
は対称行列なので直交行列
(
かつ
)で対角化可能である,
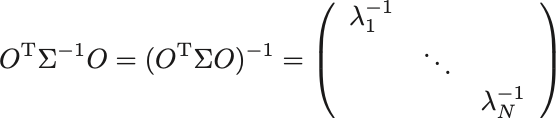
ここで は
の固有値で仮定から正の実数.
この直交行列 を用いて変数変換
を施すと,

であるから,
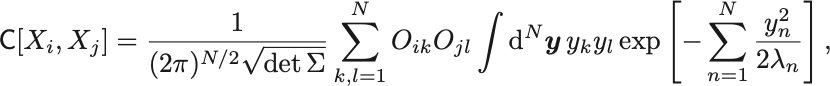
と 個のGauss積分の積に変形できる.
このGauss積分は のとき被積分函数が奇函数なので
になり,
のときは
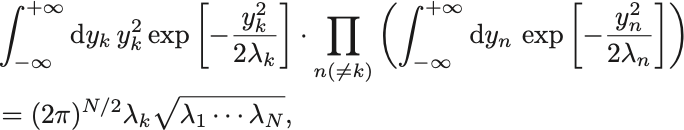
となる. の行列式は固有値を用いて
と書けることから,
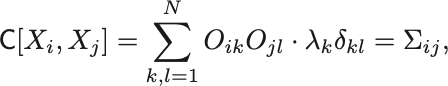
という結果を得る.
最後の等式は であることを用いた.
