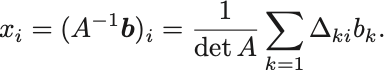Prerequisite
この節では行列からスカラーをつくる演算,行列式を紹介する.
次正方行列
の行列式 (determinant) とは
行列式
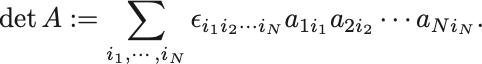
で定義されるスカラーである.
ここで は
次元のLevi-Civita記号であり
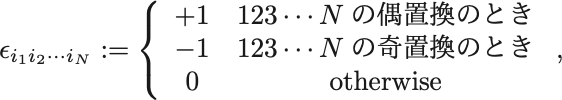
と定義される.
ここで置換の説明を簡単にしておこう. 個の数列
を並べ替えて数列を得る操作を置換 (permutation) という.
置換を とすると
ならば
である.
特に2つの数字を入れ替えるだけの置換を互換 (transposition) という.
任意の置換は互換を繰り返すことで実現でき,それは一意ではないが互換の回数の偶奇は置換に対し1つ決まる(証明は省く).
互換の数が偶数の場合は偶置換 (even) ,奇数の場合は奇置換 (odd) という.
たとえば のとき,
は偶置換,
は奇置換である.
行列式の記法として具体的な行列に対しては行列を で囲んで
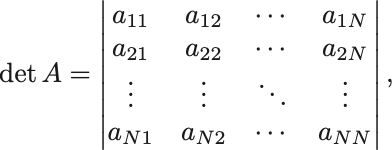
と書く.
これを踏まえて のときの行列式を具体的に書き出してみる.
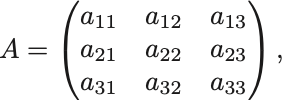
の行列式は
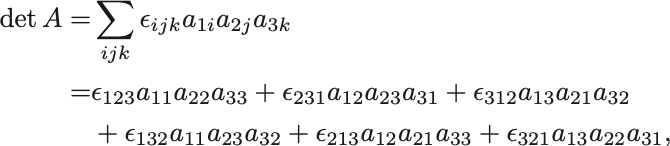
したがって
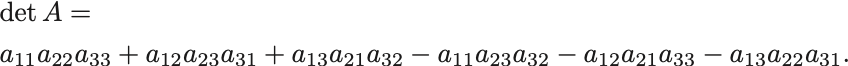
特に のときはベクトルと関係付けられる.
3次元ベクトル ,
,
とおくと行列式は
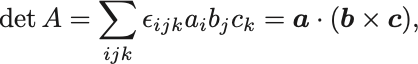
とスカラー三重積で書ける.
よって の場合は3つのベクトルが張る平行六面体の体積に等しい.
基本変形と行列式の関係を調べよう.
行列 に対して
行目を
倍して
行目に加えたもの
の行列式は
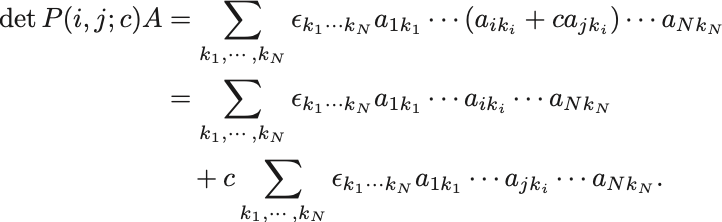
ここで1行目は に等しい.
2行目については に着目する.
Levi-Civita記号は について反対称だが
は対称である.
ゆえにこの和は相殺して となる.
したがって
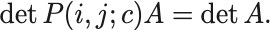
行列 に対して
行目と
行目を入れ替えた(
としても一般性を失わない)もの
の行列式は
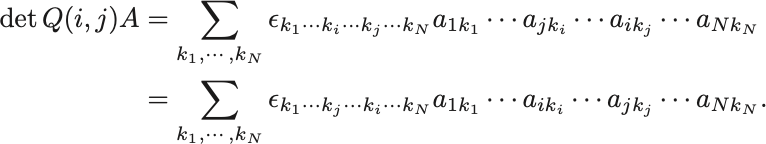
ここでLevi-Civita記号は添字を奇置換すると符号が反転するので となる.
したがって元の行列式の 倍に等しいことがわかる,
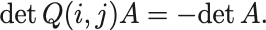
最後に行列 に対して
行目を
倍したもの
の行列式は和の各項が
倍されるだけなので
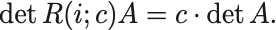
転置行列の行列式は元の行列の行列式と等しい,

証明するにはまず定義より
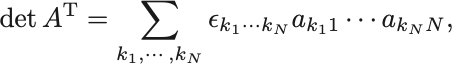
すべての項で積 を並べ替えて
にする.
このときLevi-Cicita記号 と
は等しい.
なぜならば を並べ替えて
を得るときの互換の回数と同じ回数で
から
に戻せる.

この戻す置換で は
が得られるので偶奇も等しい.
よって各項で

が成立するので所期の結果を得る.
転置行列の行列式が等しいことによって,行に関して成立する性質は列に関しても成立することを意味する.
たとえば上記で基本変形は行についてだけ見たが列についても同様である.
2つの行列 の積の行列式については次が成立する,

つまり行列の積を行列式では実数の積に置き換えられる.
証明のためにまず積の定義より
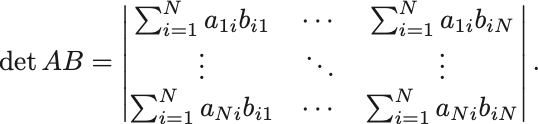
1列目に着目して行列式の線型性を使えば,

として をくくり出せる.
他の列でも同様にして

和の各項で を並び替えて
となるようにすれば行列式の部分は
に等しくなる.
このとき行列式は互換の回数だけ 倍されるので
がかかる.
よって

となり所期の結果を得る.
が正則行列のとき逆行列
が存在して
である.
であり積の性質から

がわかる.
よって が正則ならば
でなければならない.
この命題の逆については後述する.
直ちに計算が可能な行列として三角行列 (triangular matrix) がある. 次正方行列で
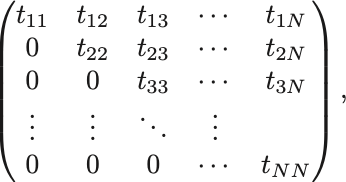
という形の行列を上三角行列といい,
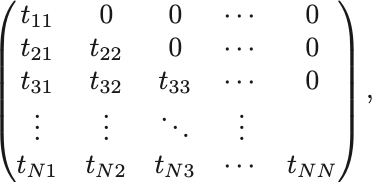
という形の行列を下三角行列という.
行列 が三角行列ならば行列式は必ず対角成分の積に等しい:
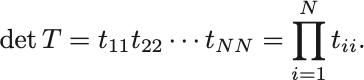
上三角行列で示す(下三角行列は転置を取ればよい).
上三角では で
なので,行列式の和の内で
でない項は
の全てが
でなければならない.
これを満たせるのは のみである.
任意の行列式を計算したい場合は基本変形を施して三角行列の形まで変形できればその行列式が求められる.
次正方行列
の行列式を1行目の成分の線形結合と見て
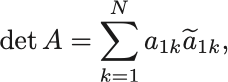
とおく.
ここで係数は
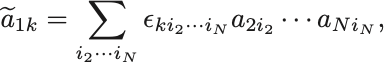
である.
は
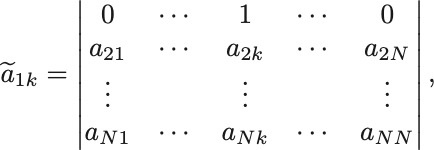
という 次行列の行列式と等しいことがわかる.
まず に着目するとLevi-Civita記号
は添字
は固定で残りの
が実質的な添字
の動く範囲なので
を落とした
に等しい.
よって
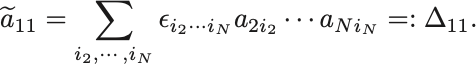
ここで は行列
の1行目と1列目を取り除いた行列の行列式,
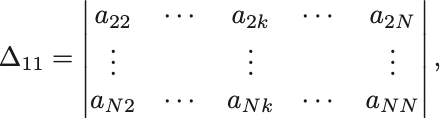
であり,行列の 余因子 (cofactor) という.
次に一般の では
列目を順々に入れ替えて1列目へ持ってくることで
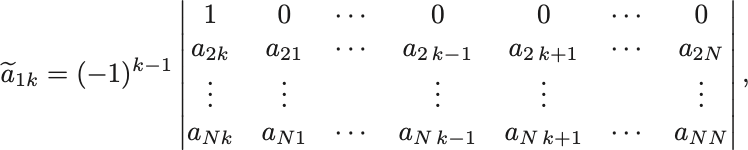
となり と同様に行列
の1行目と
列目を取り除いた行列の行列式,
余因子
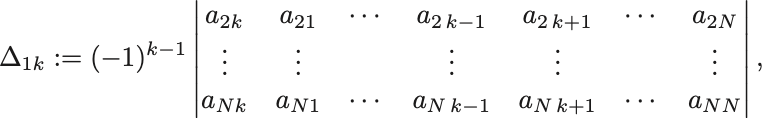
が係数となる.よって
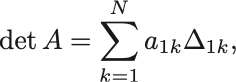
と展開できる.
今は1行目について展開したが 行目について展開した場合は
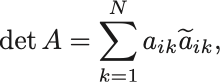
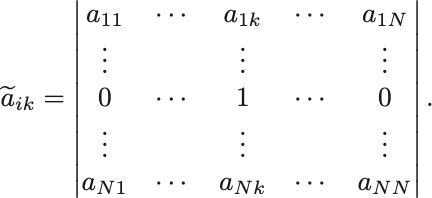
基本変形によって 行目を順々に1行目へ入れ替えて,さらに
列目を1列目へ順々に入れ替えれば
成分に
を持ってこれる.
よって行列式に がかかる以外は同じ議論により
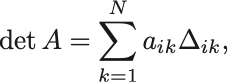
と展開できることがわかる. は行列
の
余因子という.
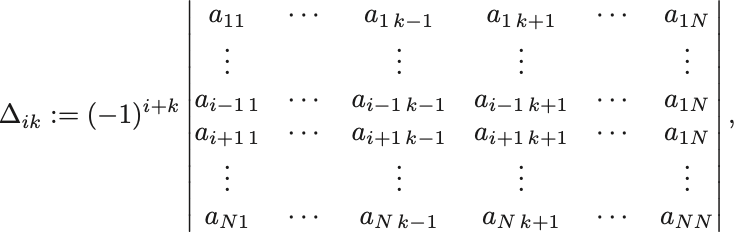
和 を考える.
のときは上の結果から
に等しい.
のときは
行目と
行目に同じものが現れる行列式に等しくなる,
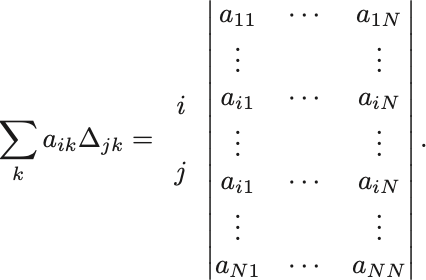
これは 行目と
行目の入れ替えで符号が変わることから
に等しいことがわかる.
以上の結果をまとめると
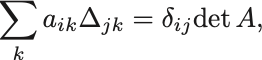
が成り立つ.
さらに行と列を入れ替えても全く同様の式が成り立つ:
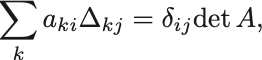
この2つを余因子展開という.
余因子を並べて転置をとった行列
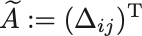
を定義すると余因子展開は

とかける.
もし ならば
の逆行列が

である.これにより次が示された:
行列 が正則
つまり行列式は行列が逆行列をもつかどうかの判定手段となる.
行列を使うと線型連立方程式を簡潔に書くことができる. 個の変数
に関する
個の方程式からなる連立方程式
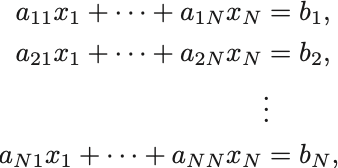
に対して,列ベクトル と
と行列
を導入すれば
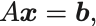
と書ける.
が正則ならば
と解くことができる.
の場合の方程式
は重要である.
この方程式は が正則ならば自明な
が解である.
したがって自明でない解,すなわち のうち少なくとも1つは
ではない解を持つためには
が必要条件である.
Problems
次の 次の正方行列
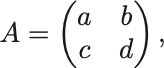
に対して逆行列を持つための実数 の条件を調べ,余因子から逆行列を求めよ.
定義にしたがって余因子は

行列式は余因子展開より
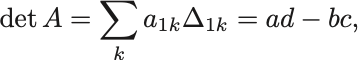
よって逆行列を持つための条件は .
逆行列は
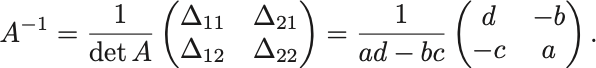
次の 次の正方行列の行列式を求めよ:
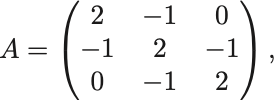
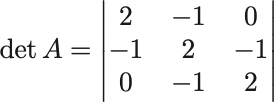
まず 行目の
倍を
行目に加える,
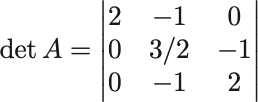
行目の
倍を
行目に加える,
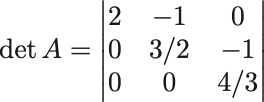
上三角行列の形なので対角成分の積で与えられる,
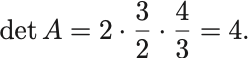
Cramerの公式: 個の変数
に関する
個の方程式からなる連立方程式
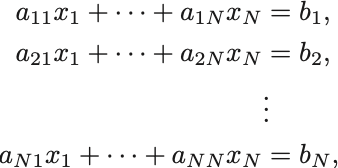
について,係数行列 が正則ならば解が
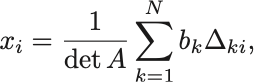
で与えられることを示せ.
連立方程式は とかける.
は正則なので逆行列が存在し
と解ける.
逆行列は余因子 を用いて

と表せるので代入して整理すれば,