場のLagrange形式

~ QuantumAtsuo

Prerequisite

三次元の空間上の場について，次のように定義されるLagrangian密度 \mathcal{L} によって作用原理を考える：

ここで \mathcal{L}=\mathcal{L}(\phi,\partial_{\mu}\phi,x) である．
一般にLagrangian密度は四次元座標 x=(ct,\boldsymbol{x}) と場 \phi とその微分の函数で書かれる．
作用積分はLagrangian密度の区間 [t_0,\,t_1] と全空間で囲まれた領域上の積分，

で定義される．

作用原理における場の境界条件

いま作用の引数は質点の軌道ではなく場の配位 \phi であることに注意．
場の配位とは時空の各点でどのような値をとっている函数なのかということである．
質点の軌道は作用を極小にするように決まったことから，同様に場の配位も作用を極小にするように決まると仮定する．
場を \phi(x)\mapsto\phi(x)+\delta\phi(x) と微小に変化させる．
そのとき時刻 t_0,\,t_1 における三次元空間 \Sigma_0,\,\Sigma_1 での場の配位は固定する．
また無限遠方においても場の配位は固定する．
言い換えると作用が定義されている四次元領域の境界で場の配位は固定しておく； \delta\phi=0 ．
そのとき作用の変分は，

第2項について部分積分を行うと，

部分積分により現れた後ろの項は四次元空間上のGaussの定理により，表面積分の項

となる．
境界で場の配位を固定する条件 \delta\phi(x)\to0 からこの表面項は 0 となる．

したがって，

場の変位 \delta\phi は任意にとってこれるからこれが成り立つためには，

が成り立たなければならない．
これが場についてのEuler–Lagrange方程式である．

例として実スカラー場のLagrangianの場合のEuler–Lagrange方程式を導いてみよう：

第1項からは運動項，

第2項からはポテンシャルの項，

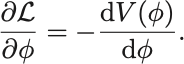
よってEuler–Lagrange方程式は，

特に K が光速 c のときにはLorentz不変な方程式，

が得られる．
\Box はd’Alembert演算子，またはd’Alembertianとよばれる．

さらに V(\phi)=m^2c^2\phi^2/2 の場合は特に名前がついていて，

をKlein–Gordon方程式といい，その解 \phi(x) をKlein–Gordon場という．
Klein–Gordon場は相対論的な量子力学において重要な役割を果たす．

Problems

\textsc{Problem1. }

\phi^4 理論: 次のLagrangianについてEuler–Lagrange方程式を導出せよ．

ただし \lambda,\,m は正の定数．

\textsc{Solution.}

以上より

\textsc{Problem2. }

sine–Gordon模型: 次のLagrangianについてEuler–Lagrange方程式を導出せよ．

ただし \lambda,\,m は正の定数．

\textsc{Solution.}

以上より

\textsc{Problem3. }

O(N)模型: 次の N 個の場 \phi_1,\,\cdots,\,\phi_N についてのLagrangianについてEuler–Lagrange方程式を導出せよ．

ただし \lambda,\,m は正の定数．
また場の添字は同じ添字が現れたとき 1 から N まで和を取っているものとする

\textsc{Solution. }

以上より

\textsc{Problem4.}

Karder-Parisi-Zhang理論: 次のLagrangianについて \widetilde{\phi} に関するEuler–Lagrange方程式を導出せよ．

ただし D,\,g は定数．

\textsc{Solution.}

以上より

Next

コメントを残す