Prerequisite
ではIsingモデルに対して統計力学の手法を用いて各種熱力学量を求めたり,その性質を調べていくことにしよう.
Isingモデルは一次元と二次元の場合には厳密解が知られているが三次元では厳密には計算できていない.
ここではまず任意次元の空間のIsingモデルについて平均場近似 (mean field approximation) を用いて計算していこう.
平均場近似とは最近接相互作用をスピン変数 の平均値
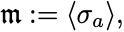
と の相互作用に置き換える近似である.
具体的にはまずスピン変数を
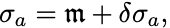
として期待値と,期待値からのずれ とに2つに分離する.
そして期待値のずれは小さく2次以上の項は無視できるとする.
IsingモデルのHamiltonianは

上の変形を相互作用の部分に代入して整理していくと

第1項の最近接ペアの和を計算するために1つのスピン に着目する.
このスピンの最近接スピンの個数を とおく.
一次元では ,二次元正方格子では
,三次元正方格子では
などなどで一般次元では
ある.
すると第1項は

と計算できる.
ただし は
を固定して格子点
におけるすべての最近接(Nearest Neighbor)格子点にわたる和を意味する(重複に注意).
また はスピン(格子点)の総数である.
次に第2項については でスピン変数に戻し,同様の和の書き換えを行えば,
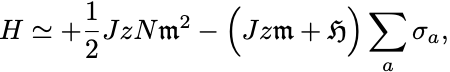
を得る.
これが平均場近似における有効Hamiltonianである.
いまスピンはあたかも有効外場

と相互作用するかのようになっている.
スピンは真の外部磁場と平均場 と相互作用する.
系のHamiltonianが簡単化されたところで分配函数を計算していこう.
二準位系の分配函数は

平均場近似のもとでは容易に計算ができて
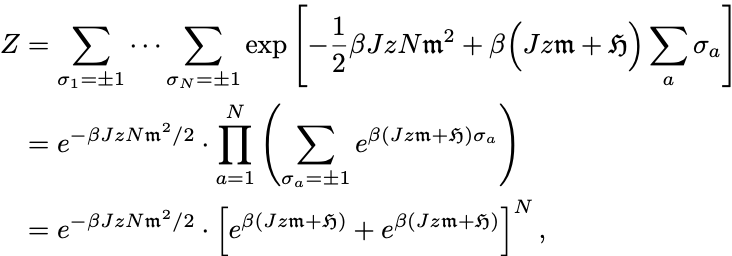
となる.
自由エネルギーは
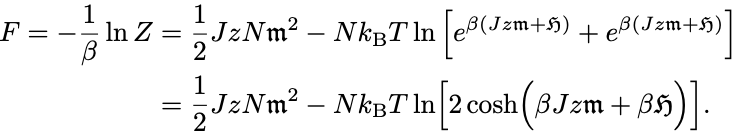
次に磁化は一様外部磁場中の熱力学から
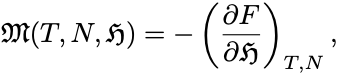
によって計算できる.
これを2通りの見方で考えよう.
まずIsingモデルのHamiltonianにおいて外部磁場 は
にのみ現れる.
そのため

によって計算するときは,指数函数の に作用し
が降りてきて
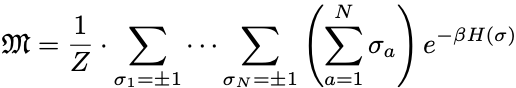
右辺はすなわち に等しい.
スピン自由度の平均値 はスピン1つあたりの磁化
に等しい.
この関係は平均場近似ではなく厳密に成り立つ式である.
もう1つは上の期待値を平均場近似Hamiltonianを用いて直接計算することによって求められて
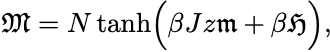
を得る.
以上から
自己無撞着方程式

という に関する方程式が得られる.
ここで は
の函数である.
この方程式は一般には熱力学量の間の関係を定める状態方程式であるが,平均場理論の文脈では自己無撞着方程式 (self-consistent eqation) と呼ばれる.
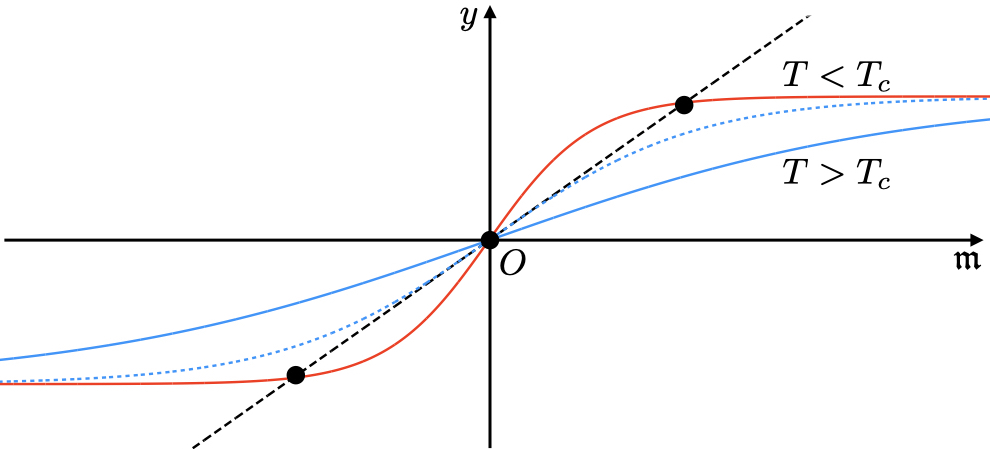
平均場近似のIsingモデルは強磁性-常磁性転移の臨界現象を記述することができる.
この転移は外部磁場が印加されていないときに起こるのでまずは としよう.
次に2つのグラフ と
の交点の問題を考えよう.
この2つは のとき交点は3つ存在し,
のとき交点は1つだけとなる.
そして3つ存在するとき の2つの交点はちょうど原点対称な位置にある.
なので
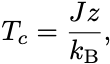
とおけばこの温度 を境に解の個数が変わることになる.
そして で
のみのときが常磁性相,
で解が
の解も存在するときが強磁性相に対応する.
そして が臨界点といえる.
次にIsingモデルの平均場近似での臨界指数 を求めたい.
最初に転移点直上 において自己無撞着方程式を調べよう.
逆双曲線函数を用いて
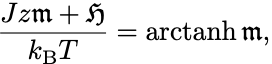
と変形できる.
外部磁場は弱いならば誘起される磁化も小さいので により,
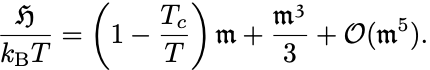
ゆえに において
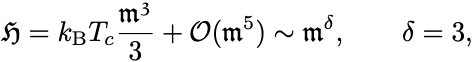
となる.
転移点近傍 で自発磁化
は小さいと仮定できるので自己無撞着方程式の右辺を展開して
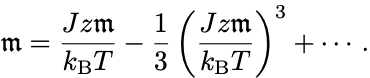
3次までで考えて, として両辺割って整理すれば
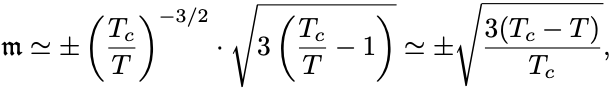
となる.
註)転移点近傍でかつ転移点以下 の強磁性相を考えるので,
は微小量であり
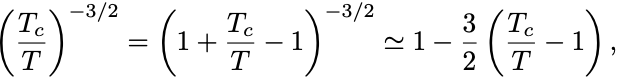
と評価できることに注意せよ.
また と変形して同様の近似により
と評価している.
このような近似は後の計算にも頻繁にも用いる.
よって臨界指数は
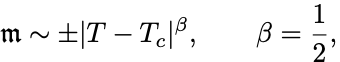
である.
等温磁化率は

と定義される.
転移点近傍の等温磁化率のふるまいを調べるには自己無撞着方程式の両辺を外部磁場で微分すれば良い.
この方程式で磁化が の函数であることに注意して
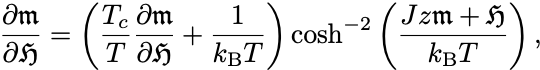
となる.
常磁性相 では自明な解
なので

である.
強磁性相 では
なので
であることを用いて
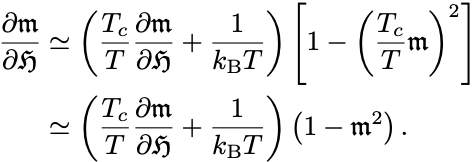
の1次までを残して整理すると
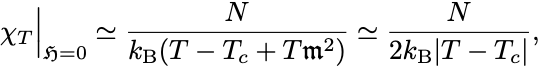
すなわち
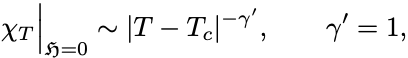
を得る.
常磁性相と強磁性相の係数の比はちょうど である.
最後に転移点近傍の比熱を求めたい.
磁性体の比熱は

で定義される.
常磁性相では自発磁化がないので で比熱も
となる.
よって発散はなく .
強磁性相では であることと自己無撞着方程式を用いて
を消去できて
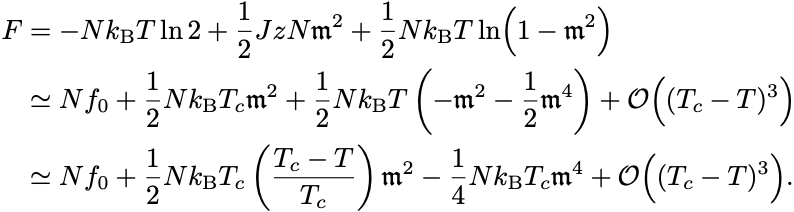
ここで は比熱に影響しない磁化の
次の項.
を代入して
の冪で2次までで整理すると
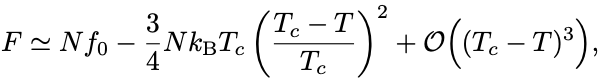
となる.
註)厳密には系には2つの解に対応した磁区が生じていて,それらを部分系とみなしたときの自由エネルギーの総和である.
しかし外部磁場がないとき自由エネルギーは磁化に関して偶函数のためにこのことを考慮しなくても同じ結果を与える.
これから比熱は直ちに計算できて

がわかる.
以上の結果をまとめるとIsingモデルの平均場理論では
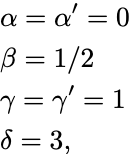
であった.
これは強磁性転移のLandau理論と同じ結果である.
そのことを確かめるために自由エネルギー をLegendre変換して
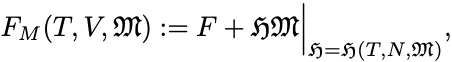
を定義する.
こちらは温度以外が示量変数の通常のHelmholtz自由エネルギーである.
平均場近似の自由エネルギーと状態方程式を代入して転移点近傍では
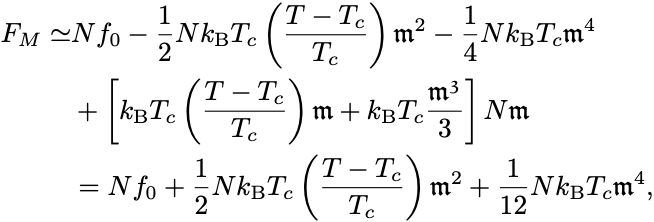
となる.
これはLandau理論で仮定した自由エネルギーの表式と一致していて,磁化の二次の係数の符号によって相転移が記述される.
したがってIsingモデルの平均場近似は臨界指数のレベルではLandau理論と等価である.
