ベクトル解析の公式

Prerequisite

ベクトル解析の基礎

ベクトル場の微分に関してはいくつかの公式が知られている．
また物理において重要な役割を果たすことが非常に多いため，それらの式と証明をここで与えておく．
表記の簡単のためにEinsteinの縮約規則を採用し，1つの項に同じ添字が現れたときは和をとっているものとみなす．
また微分は

と略記する．

スカラー場の積 $fg$ の勾配はLeibniz則

を満たす．
成分で書けばふつうの微分だから

により直接確かめられる．
同様にスカラー場とベクトル場の積 $f\boldsymbol{A}$ の発散と回転に関しても同様に，

が成り立つことがわかる．
成分で書けば容易く確かめられて

2つのベクトル場の外積 $\boldsymbol{A}\times\boldsymbol{B}$ の微分は，

となる．
なぜならば発散については，

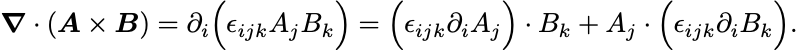
第2項でLevi-Civita記号の添字を $\epsilon_{ijk}=-\epsilon_{jik}$ と入れ替えればよい．
次に回転の方の左辺の $i$ 成分は，

となって右辺の $i$ 成分に等しい．

2つのベクトル場の内積 $\boldsymbol{A}\cdot\boldsymbol{B}$ の勾配については，

となる．
右辺の $i$ 成分を計算すると，

となって左辺を得る．

では次に2階微分を調べよう．
スカラー場の勾配 $\boldsymbol{\nabla} f$ の発散と回転は，

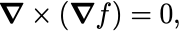
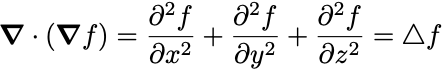
ここで微分演算子 $\triangle$ をLaplace演算子，またはLaplacianという．
1つ目の左辺が $\epsilon_{ijk}\partial_j\partial_kf$ とかけるので $0$ に等しい．
2つ目の方は定義から書き下せばよい．

ベクトル場 $\boldsymbol{A}$ の発散の勾配は

で特に変形はできない．
ベクトル場 $\boldsymbol{A}$ の回転の発散と回転の回転は，

となる．
これらはベクトル場の外積の微分の公式を示すときと同じようにして示すことができる．
回転の発散については

となるが微分の可換性とLevi-Civita記号の反対称性からこの縮約は $0$ に等しい．
回転の回転の $i$ 成分は

となって第1項で微分を入れ替えれば所期の結果を得る．

[スカラーポテンシャルの存在条件]

Stokesの定理に着目する:

境界 $\partial S$ は任意に選ぶことができる．
空間内の任意の2点 $\boldsymbol{x}_1,\,\boldsymbol{x}_2$ をとる．
あるベクトル場 $\boldsymbol{A}(\boldsymbol{x})$ が任意の曲線に沿った線積分で値が変わらないとすると，2点を結ぶ任意の2つの曲線 $\gamma_1,\,\gamma_2$ に対し

が成り立つ．
$\gamma_1$ と $\gamma_2$ の逆向きの曲線を繋いでループ $\partial S$ での周回積分に書き換えれば

となる．
すなわち端点を固定した線積分が間の経路に依存しないことは，任意のループに沿った線積分が $0$ となることと同値である．
さらにStokesの定理によりループが囲む曲面に関して

となる．
この曲面を無限小にする極限がとれる（曲面に穴がない）とき

が任意の点 $\boldsymbol{x}$ で成立する．
このときベクトル場 $\boldsymbol{A}(\boldsymbol{x})$ は渦なしという．
逆にベクトル場が任意の点で渦なしであればその線積分の値は端点の座標にのみ依存し，間の経路に依存しない．

ところでベクトル場の線積分が経路によらないとき適当な基準点 $\boldsymbol{x}_*$ を選んで，

という量を経路によらず定義できる．
すると任意の2点 $\boldsymbol{x}_1,\boldsymbol{x}_2$ での差をとると

他方で2点を結ぶ経路を1つとってパラメータ $t$ を入れると左辺は

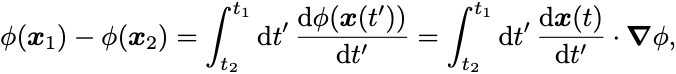
となる．
経路の式を変数変換 $\boldsymbol{x}=\boldsymbol{x}(t)$ と思えば線積分

と変形できる．
したがってベクトル場 $\boldsymbol{A}$ にはスカラーポテンシャル $\phi$ が存在して

と（定数を除いて）書くことができる．
このときたしかに $\boldsymbol{\nabla}\times\boldsymbol{A}=\boldsymbol{\nabla}\times(\boldsymbol{\nabla}\phi)=0$ が成立している．
よって逆の問題

が導かれる．

この事実は物理にしばしば登場する．
Newtonの運動方程式

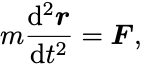
においてエネルギーが保存するための条件は力 $\boldsymbol{F}$ に対しポテンシャルエネルギー $V(\boldsymbol{x})$ が存在して

と書けることである．
このとき仕事は

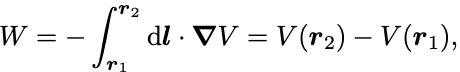
となって仕事も途中の経路に依らず，始点と終点でのポテンシャルの値によってのみ決まる．
このとき運動方程式に速度をかけて積分することで

となり力学的エネルギー保存則の式が導かれる．
力学的エネルギーが保存するための条件は力 $\boldsymbol{F}$ が渦なし $\boldsymbol{\nabla}\times\boldsymbol{F}=\boldsymbol{0}$ を満たすことである．

電磁気学では静電場 $\boldsymbol{E}(\boldsymbol{x})$ について渦なしの条件 $\boldsymbol{\nabla}\times\boldsymbol{E}=\boldsymbol{0}$ が満たされる．
したがって静電ポテンシャルが存在して $\boldsymbol{E}=-\boldsymbol{\nabla}\phi$ と書くことができる．

[ベクトルポテンシャルの存在条件]

今度はGaussの定理に着目する:

境界 $\partial V$ は任意に選ぶことができる．
空間内に境界が一致した2つの任意の曲面 $S_1,\,S_2$ をとる．
あるベクトル場 $\boldsymbol{A}(\boldsymbol{x})$ について，その面積分が境界のみに依存し内部の曲面の形状に依存しないとすると，

が成り立つ．
$S_1$ と $S_2$ を反転した曲面を繋いで閉曲面 $\partial V$ での積分に書き換えれば

となる．
すなわち境界を固定した面積分が内部の曲面の形状に依存しないことは，任意の閉曲面上の面積分が $0$ となることと同値である．
さらにGaussの定理により閉曲面が囲む3次元領域 $V$ に関して

となる．
この領域を無限小にする極限がとれる（曲面に穴がない）とき

が任意の点 $\boldsymbol{x}$ で成立する．
このときベクトル場 $\boldsymbol{A}(\boldsymbol{x})$ は湧き出しなしという．
逆にベクトル場が任意の点で湧き出しなしであればその面積分の値は境界のみに依存し，内部の曲面の形状に依存しない．

スカラーポテンシャルと同様に逆問題を考えたい．
ここではいわゆる星形領域に制限して示そう: いま $\boldsymbol{A}(\boldsymbol{x})$ の定義域はその中の任意の点と原点を結ぶ線分を必ず含むと仮定する．
このときやや天下りであるが湧き出しなしのベクトル場 $\boldsymbol{A}$ から新たなベクトル場

が定義できる．
この積分は原点と任意の点 $\boldsymbol{x}$ を結ぶ線分に沿った積分である．
このベクトル場の回転を計算すると

第1項では $\epsilon_{ijk}\epsilon_{klm}\delta_{jl}=-\epsilon_{ijk}\epsilon_{mkj}=-2\delta_{im}$ となる．
第2項では鎖法則より

となって，前の $\epsilon_{ijk}\epsilon_{klm}$ に対してLevi-Civita記号の公式を適用すれば

第2項では湧き出しなしの条件 $\boldsymbol{\nabla}\cdot\boldsymbol{A}=0$ なので落とせる．
第3項は $t$ 微分で書けば

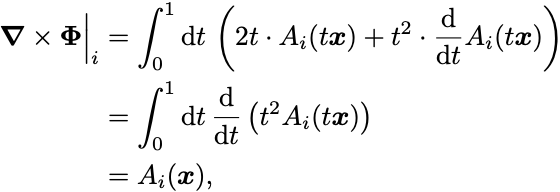
となる．
すなわち

が成り立つ．
この $\boldsymbol{\Phi}$ をベクトルポテンシャルという．
このときたしかに $\boldsymbol{\nabla}\cdot\boldsymbol{A}=\boldsymbol{\nabla}\cdot(\boldsymbol{\nabla}\times\boldsymbol{\Phi})=0$ が成立している．
よって逆の問題

が導かれる．

ベクトルポテンシャルは磁場 $\boldsymbol{B}$ において導入した．
磁場は単磁荷の非存在の式 $\boldsymbol{\nabla}\cdot\boldsymbol{B}=0$ からただちにベクトルポテンシャル $\boldsymbol{B}=\boldsymbol{\nabla}\times\boldsymbol{A}$ とおくことができる．