Prerequisite
この節では行列に関する固有値問題を議論する.
固有値問題は物理において頻繁に現れる問題で,量子力学においてはまさに基礎方程式が固有値問題である.
ただしここでは一般論は議論せず実対称行列に限定する.
複素行列の固有値問題については量子力学の章で詳説する.
一般に 次正方行列
に関する固有値問題とは

を満たすスカラー と零ベクトルでないベクトル
を求めることである.
その の解を固有値 (eigenvalue) ,
の解を
に属する固有ベクトル (eigenvector) という.
右辺に単位行列が作用しているとして とすれば,

と変形できる.
この方程式で であるための条件は行列
に逆行列が存在しないことである.
よって
固有方程式
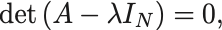
が成り立たなければならない.
この に関する方程式を固有方程式という.
固有方程式は一般に の
次の多項式でありその根は代数学の基本定理よりたかだか
個である.
重根がある場合は物理では縮退 (degeneracy) があるという.
固有方程式を解いて固有値 を得たら,元の方程式
を解いて固有ベクトル
を定めることができる.
この節では実対称行列に限定する.
対称行列とは転置をとっても不変であり, を満たす行列のことである.
一方で転置して符号が反転する行列 は反対称行列という.
特に成分がすべて実数の対称行列を実対称行列という.
まず実対称行列の固有値は全て実数であることが示せる.
固有値方程式 の両辺で複素共役をとると
が成り立つ.
このときベクトル と
の内積を取ると

一方で対称行列であることから,

2つを合わせると

となるが なので
でなければならない.
固有値が実数なので固有ベクトルも実ベクトルとして求まる.
今は縮退はないとして 個の固有値
は全て相異なるとする.
2つの固有値 とそれぞれに属する固有ベクトル
を考える.
ベクトル と
の内積を取ると
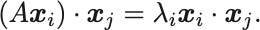
一方で対称行列であることから,

2つを合わせると
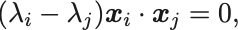
となるが なら
なので
でなければならない.
すなわち異なる固有値に属する固有ベクトルは直交する.
この直交性は縮退がある場合にも同様に成立する(証明略).
固有ベクトルはスカラー倍の不定性がある.
そこで慣習的に固有ベクトルの大きさを にとることが多い:
. この2つを合わせると実対称行列の固有ベクトルを

を満たすように選べる.
固有ベクトルを列にもつ 次正方行列
をつくる.
この行列の転置 との積をとると

両辺の行列式を取ると より
なので
は正則で逆行列
が存在する.
の右から
をかけると
がわかる.
となる行列を一般に直交行列 (orthogonal matrix) という.
さてこの直交行列 を使って
を計算すると,

となる.
固有ベクトルの直交性から結局
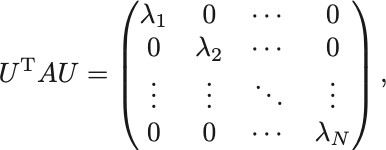
を得る.
実対称行列 の固有ベクトルからつくった直交行列
を使って
は対角成分に固有値が並びそれ以外は
の行列を得ることができる.
これを行列の対角化といい,実対称行列の場合は必ず直交行列によって対角化可能である.
すべての行列が対角化可能ではないことに注意せよ.
成分が の対角行列を記号で

と書くことがある.
対角化行列の行列式は

である.
直交行列の行列式の2乗は に等しいから

が成立する.
Problems
次の 次の実対称行列を固有値,固有ベクトルを求めよ:

また を対角化する直交行列
を求めよ.
まず固有値を求めるために固有値方程式 を解く.
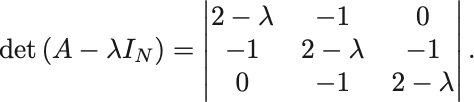
1行目についての余因子展開より
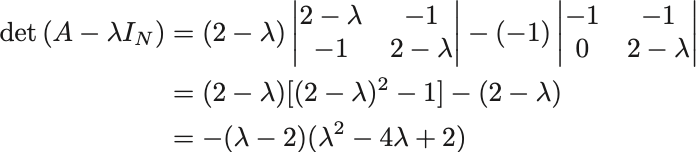
よって固有値は .
次にそれぞれの固有値に属する固有ベクトルを求める. のとき,
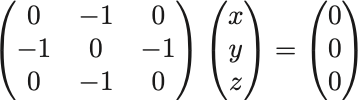
これを解くと .
大きさ を課せば固有ベクトルは
と求まる.
同様にして の場合も固有ベクトルを求めると
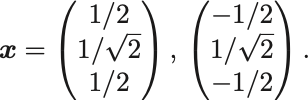
直交行列

は行列 を対角化する.
