Diracは量子力学の構成のために都合の良いものとして次で定義される函数 を持ち出した:
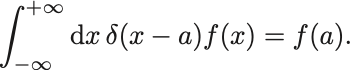
ここで はなめらかな任意の函数,
は定数である.
これをDiracのデルタ函数という.
デルタ函数が積分の中にあらわれると,一緒に積分した函数のデルタ函数の引数が になるところの値が返ってくるのである.
また の
以外のところの値がなんであれ
しか与えないということは,
ということを意味する.
そうでなければ函数によって返す値は異なってしまう.
また の1点でのみ積分が有限の値を持つためには
でなければならない.
すなわち,
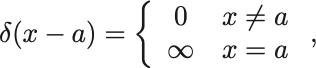
というように考えることもできる.
さらにデルタ函数は積分範囲にも依存しない.
積分範囲は をまたぐようにとればよい.
逆に積分範囲が をまたがないときには積分の値は
に等しくなる.以下では基本的に積分による定義にしたがうことにする.
このように定義される函数をふつうの函数と区別してSchwarz超函数 (distribution) という.
まずはデルタ函数の性質をいくつか挙げておこう.
まず偶函数で
デルタ函数の性質 (1)
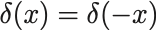
を満たす.
超函数の等号を示すには任意の函数 との積の積分が同じ振る舞いをすることを示せば良い.
すなわち,
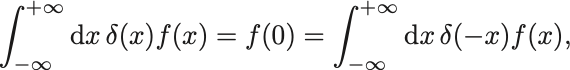
であるので示されたことになる.
次に引数について をなめらかな函数とすると,
デルタ函数の性質 (2)
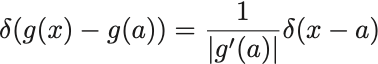
が成り立つ.
証明は変数変換 をすると,
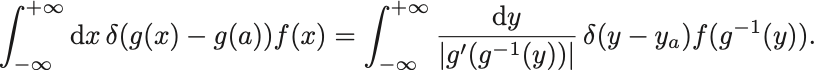
ここで である.
デルタ函数の定義より右辺は に注意して,
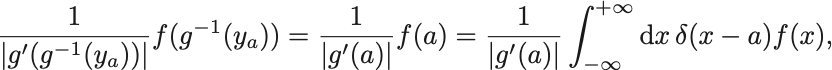
となって示された.
ここでは なる解を
のただ1つと暗に仮定したが一般には複数存在する.
そこでそれらを とおいてその近傍での積分に分ける:
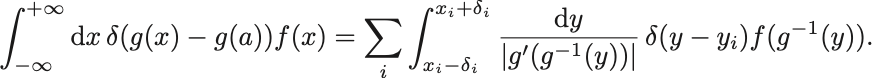
ただし .
そうして公式,
デルタ函数の性質 (2)’
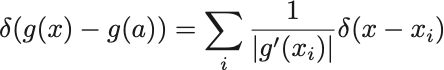
が得られる.
たとえばよく用いられるのは の場合で,
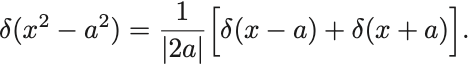
次元に関しては, が長さの次元
を持つならば左辺のデルタ函数は
の次元を持つ.
一方右辺のデルタ函数は なのが前の係数により全体として
の次元を持って,両辺の次元が一致する.
デルタ函数のFourier変換は,
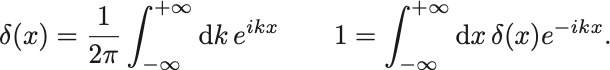
この等式を示すには のFourier変換を利用して,

となるのでデルタ函数と同じ振る舞いをする.
デルタ函数はKroneckerのデルタを連続変数に拡張したものであることに注目しよう.
Kroneckerのデルタとは,
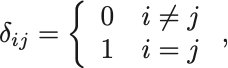
によって定義されるものである.
デルタ函数との対応が明らかになるように書くと,
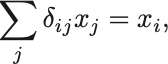
となる.
[デルタ函数の表現]
デルタ函数にはいくつかの別の定義があり,それらはすべてはじめの定義と同値である.
まず1つ目はGaussianによる定義である:
デルタ函数の表現(1)

極限の中はピークの高さが で幅が
程度のGaussianである.
の極限をとると高さが無限大,幅が0に近づく.
直感的にもデルタ函数に近づくことがわかる.
計算で確かめると,
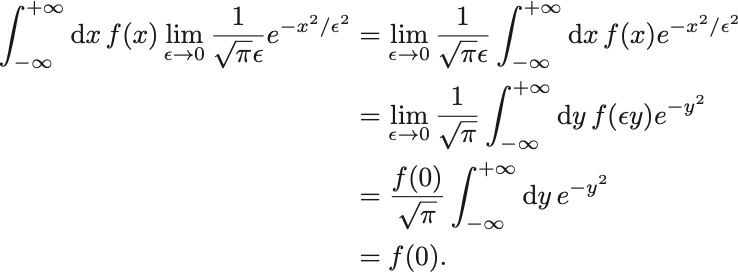
よって示された.
途中で変数変換 を行った.
次に,Lorenzianによる定義:
デルタ函数の表現(2)
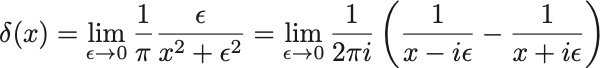
これはもっと一般的な佐藤超函数としての定義になっている.
極限の中の函数のグラフはGaussianとほぼ同じ形をしている.
計算によって等号を示すには の変数変換を行うと,
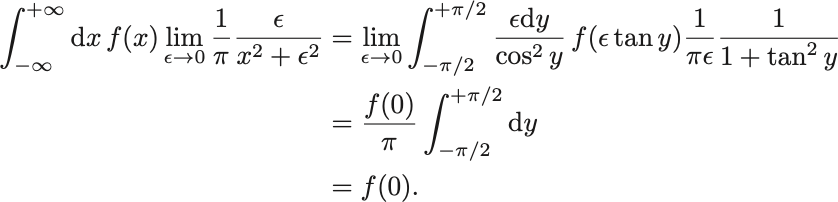
よって示された.
虚部を用いて次のようにもかける:

極限の中の函数を実部と虚部に分けると,
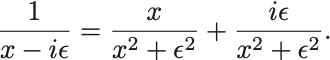
の極限では,
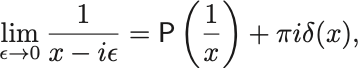
となる.
ここで は主値積分を表す.
主値積分も一つの超函数であり, を正則な(特異点のない)函数として,

で定義される.
すなわち は
に特異点をもつのでその部分を積分範囲から除き,あとで両方から同じ速さで除いた部分を狭めるようにして定義する.
こうすると積分は有限にとどめることができる.
この右辺も超函数であるのでやはり積分で定義される.
Lorenzianによるデルタ函数の表示を用いず直接示すには複素積分,
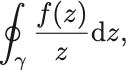
を考える.
この積分の範囲を分けて,
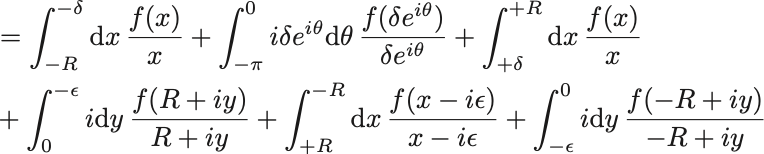
第1項と第3項は の極限で主値積分に一致する.
第4項と第6項の積分範囲では被積分函数は正則なので の極限でおちる.
第5項は の極限でいま求めたい等式の左辺に一致する.
最後に第2項は,
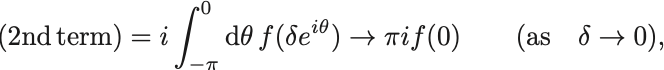
となり, はデルタ函数との積分で書き直せる.
またCauchyの積分定理よりこの複素積分は に等しい.
以上から,
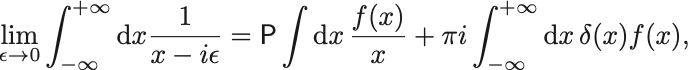
となって超函数としての等号が示された.
ところで左辺は極限を実行してしまえば になる.
函数 は
に特異点をもっているので
の定義域が
をまたぐときには注意が必要となる.
そこで を分母に入れておくことで極を虚軸の方向へ避けることができる.
そして計算した後,勝手に導入したこのパラメータ がちいさい極限をとって極限値が存在するなら以上の計算は意味を持つのである.
このような発散を避ける操作をFeynmanの 処方という.
最後にsinc函数による定義,
デルタ函数の表現(3)

極限の中の函数は原点付近で最も激しく振動し原点から遠ざかるにつれ振動が弱くなる函数である. の極限をとると原点付近でのみ激しく振動したまま残りそれ以外のところは振幅が
になってデルタ函数に近づく.
デルタ函数と等しいことを示すために,

複素解析による計算から最後の積分の値は ともとまるので証明が完了する.
デルタ函数のFourier変換の式において次のように一度積分範囲を有限で止めて後から極限をとるという形で表そう:
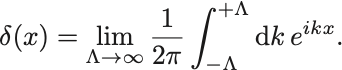
すると後ろの積分は実行できて,
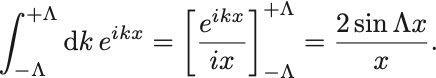
すなわち,
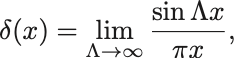
となってやはりこの表示が得られる.