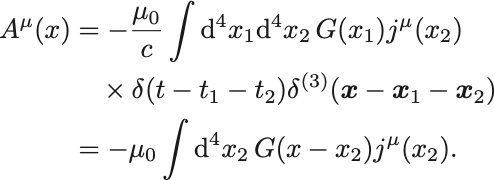Prerequisite
この節では物質があるときのMaxwell方程式

を解いていこう.
Lorenzゲージ をとって

とする.
境界条件としては無限遠で場の値が であることを課す:

非斉次の微分方程式の一般解は特解と斉次の微分方程式の一般解の和で書ける.
斉次の微分方程式はすなわち波動方程式であり,一般解は

で与えられる.
これは輻射ゲージで解いているが,Lorenzゲージの条件も同時に満たす.
特解を見つけるためにGreen函数の方法を用いる.
Maxwell方程式に対するGreen函数を

で導入する.
Green函数とデルタ函数ののFourier変換
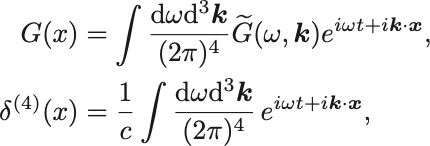
を代入すればd’Alembertianは指数函数にのみ作用して
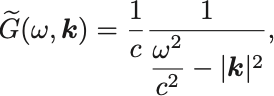
を得る.よって

の積分を計算すればGreen函数が求まる.
積分に注目すると,この被積分函数は
に極をもっている.
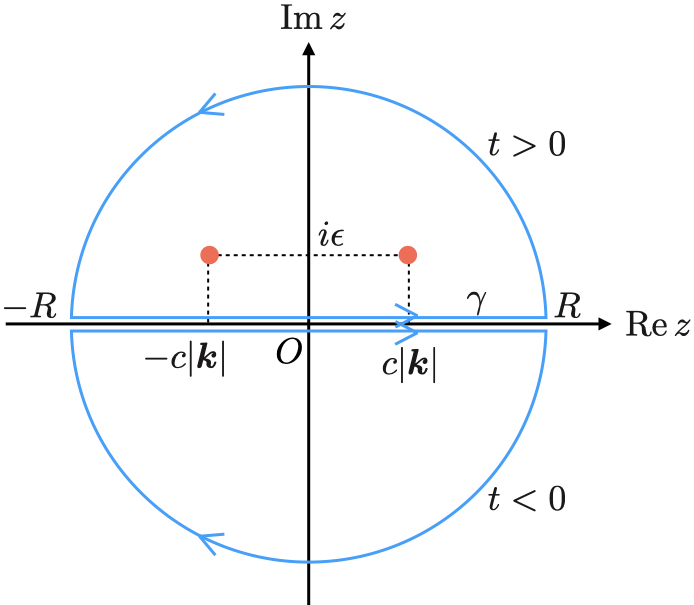
そこで複素函数
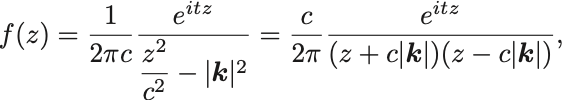
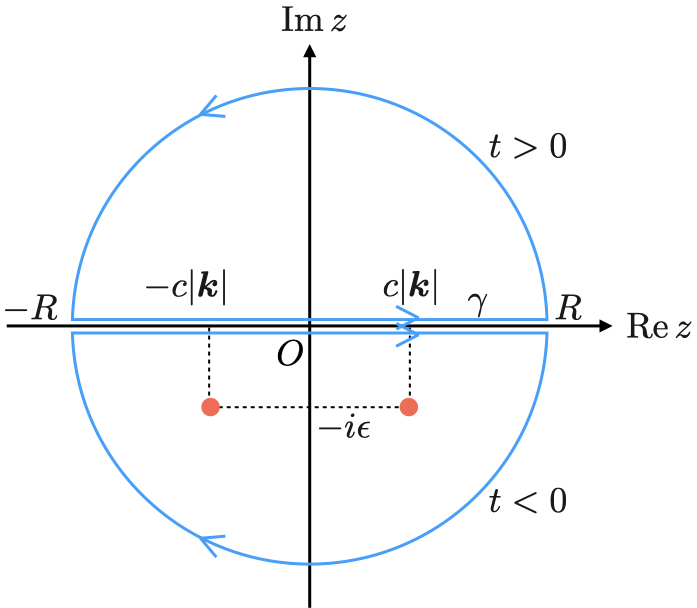
を考え図のような積分経路 をとる.
積分径路上に極があるのを避けるために次のトリックを使って計算をする;
無限小の虚数 を加えて極を虚軸方向へずらして

とする.
ただし .
また径路を閉じるために半径無限の半円をとりたいがそれには注意が必要である.
Jordanの補助定理の適用には の符号が関係している.
の場合は上半面の無限遠で半円を描いて径路を閉じれば,この半円からの寄与は落ちる.
上半面で閉じた場合径路内部に極が2つ存在するので留数定理から,

留数を計算すると なので
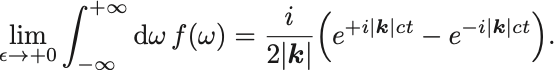
他方で の場合は下半面で閉じればこの半円からの寄与はJordanの補助定理により落ちる.
下半面で閉じた場合径路内部に極は存在しないのでCauchyの積分公式から に等しい.
したがって
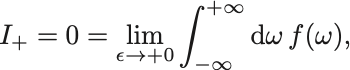
となる.
以上から
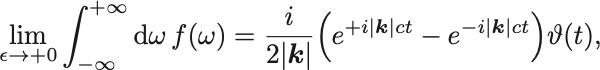
がわかった.
ここで はHeavisideの階段函数.
Green函数の残りの計算を続けよう.
今は

まで求まっている.
球面極座標をとって積分を計算していくと,

2行目から3行目へは の置き換えをして積分をまとめた.
4行目へはデルタ函数のFourier変換を用いた.
階段函数により のみ値を持ちデルタ函数の引数が
なので第1項は常に
となる.
また第2項のデルタ函数の引数が となるのは
のときのみなので階段函数の役割と重複している.
したがって
遅延Green函数

が求めるGreen函数であり,遅延Green函数という.
遅延Green函数を用いてMaxwell方程式の特解は
遅延ポテンシャル

と書くことができる(問題参照).
これは遅延ポテンシャル (retarted potential) と呼ばれる.
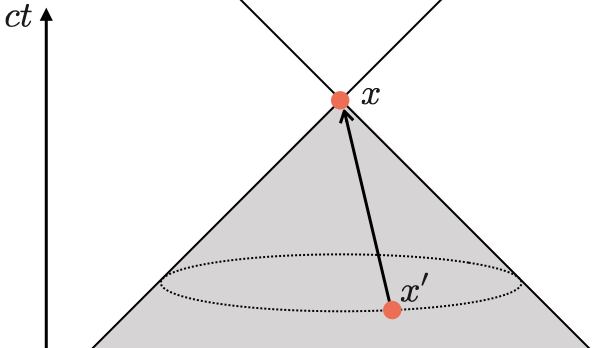
この解の意味について考えてみる.
積分中のデルタ函数によって光円錐 を満たす点
のみが積分される.
つまり観測点 より過去側の光円錐上の点
における物質の情報
が光速で
へ伝搬し
を決定していると解釈できる.
それ以外の点の物質の情報は における電磁場と因果関係にない.
電磁場と物質の相互作用は光速で行われ,相対論的な因果律の構造に則っていると言える.
Green函数の導出で用いた だけ極をずらすトリックについて再考する.
というのも極のずらし方は実軸から外れれば良いので,虚軸の上側か下側かは任意である.
遅延ポテンシャルでは2つとも上側へずらした.
2つとも下側へずらす場合は,

を計算することになる. では極が存在せず
であり,
では2つ極が存在するので留数定理から,

ここで積分経路が時計回りなので負号がつくことに注意せよ.
よってこの場合のGreen函数は同様の積分計算により

階段函数により のみ値を持ちデルタ函数の引数が
なので第2項は常に
となる.
また第1項のデルタ函数の引数が となるのは
のときのみなので階段函数の役割と重複しているので,
先進Green函数

こちらは先進Green函数といい,導かれる特解を先進ポテンシャル (advanced potential) という.
先進ポテンシャルの場合は観測点 より未来側の光円錐上の点
における物質の情報
から逆算して
を決定していると解釈できる.
ここでは詳細に触れないが極の片方を上側,もう片方を下側へずらしたGreen函数も考えられる.
これはFeynmanの 処方として知られていて,場の量子論における径路積分の境界条件と密接な関係にある.
またここではLorenzゲージを採用したがゲージ固定があらわなGreen函数を求めることも重要である.
Green函数の重ね合わせで電磁ポテンシャルがかかれるので のゲージ固定はGreen函数にも適用される.
場の量子論ではGreen函数がゲージ固定された部分空間への射影演算子としての役割を持つように扱う.
詳細は場の量子論の章で議論する.
Problems
Maxwell方程式の特解が

でかけることをFourier変換することで導け.
Fourier変換により

これらをMaxwell方程式に代入して
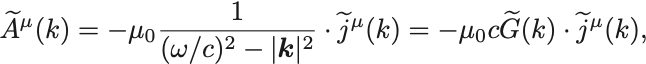
を得る.
したがって

それぞれ逆Fourier変換によって
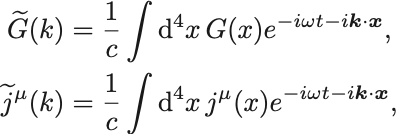
を代入すれば( のため前に
の因子があることに注意)
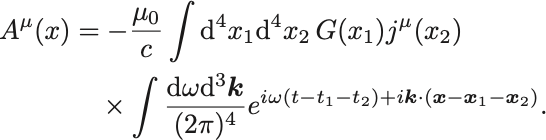
積分はデルタ函数を与えるから,