強磁性転移のLandau理論

Prerequisite

この節では連続相転移の重要な例である強磁性転移について述べる．
強磁性転移の理論は物性分野のみならず現代の物理学の全分野において重要である．

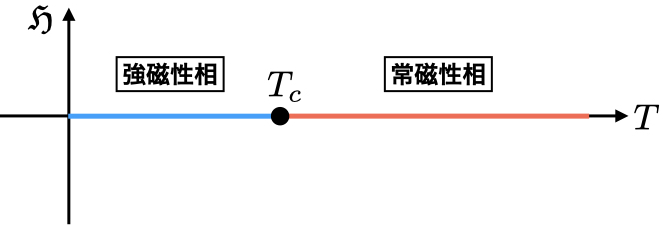
強磁性転移の相図．考えている連続な転移は $\mathfrak{H}=0$ で起こる．

強磁性転移の相図．考えている連続な転移は $\mathfrak{H}=0$ で起こる．

外部磁場に応答して磁化が生じる物体を常磁性体という．
常磁性体の温度を下げていくとある温度において自発磁化を持つ強磁性体へ相転移する．
外部磁場があると常磁性体も磁化をもつが強磁性体では外部磁場がなくても磁化が生じる（永久磁石）．
この温度は強磁性体のCurie温度 (Curie point) と呼ばれる．
この常磁性相から強磁性相への相転移は一般に連続転移であり，転移の前後で磁化は $0$ から有限の値へ連続に変化する．
しかし比熱などの量に特異性が現れることが知られているので二次転移に分類される．

一様外部磁場 $\boldsymbol{\mathfrak{H}}$ における磁性体の自由エネルギーは

$\boldsymbol{\mathfrak{M}}$ は磁性体に生じる磁化である．
議論の簡単のため粒子数は固定しておき体積の変化も考えないものとする； $\mathrm{d} N=0$ ．
さらにベクトル量を扱うのを避けるため一次元の系を考え，磁場と磁化をLegendre変換した自由エネルギーを扱う．
では磁性体の自由エネルギー

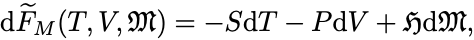
に対して議論を進めていこう．

強磁性体の状態方程式が得られれば，それについての特異性を解析することで相転移を記述することができるだろう．
しかしこの節では状態方程式のようなモデルに立脚するのではなく，系の対称性から出発する．
常磁性相においてもミクロに見れば各点で磁化は有限の値を持つが，それらはバラバラな向きなので全体としては磁化は $0$ となる．
それが外部磁場と相互作用して同じ向きを向きやすくなると系全体としてその方向の磁化が顕然すると素朴には考えられる．

この考え方でいくと強磁性相とは外部磁場がなくても磁化が同じ向きにそろいやすい状態である．
しかしどの向きにそろいやすいかというのは（物質が等方的ならば）対称である．
一次元の系ならば正と負の2つの向きがありどちらにそろいやすいかは決まらない．
熱ゆらぎやミクロな外部からの摂動によって実現する自発磁化の向きが決まる．

この経験則から強磁性転移を記述するモデルは磁化 $\mathfrak{M}$ について向きによらないことが必要である．
そこで自由エネルギーを

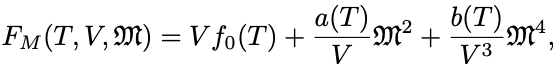
と $\mathfrak{M}$ についての偶函数を4次までのTaylor展開したもので仮定しよう．
体積 $V$ の依存性は自由エネルギーの示量性によって決まっている（今は体積変化も考えないのでこれを粒子数 $N$ にかえても同じ）．
自由エネルギーは最小値をもつから温度によらず $b(T)>0$ でなければならない．
磁化について微分すれば状態方程式

を得る．

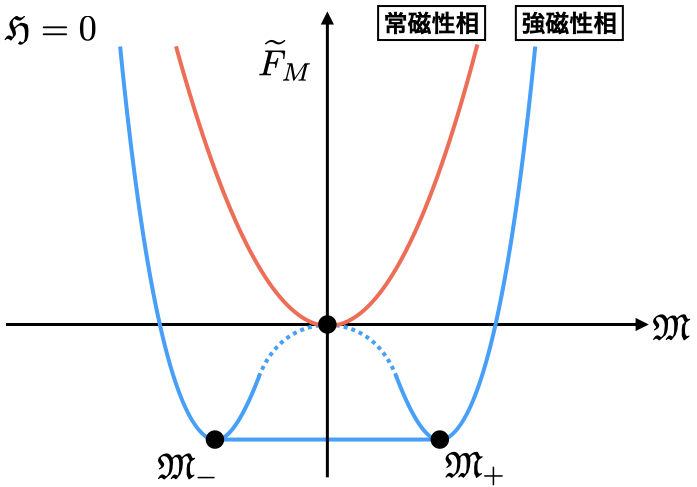
外部磁場がないときの二次の係数 $a(T)$ に着目する．
$a(T)\geq0$ の場合，自由エネルギーは磁化について下に凸な函数であり，最小値は $\mathfrak{M}=0$ において $F_M=Vf_0$ である．
これは常磁性相が対応する．
他方で $a(T)<0$ の場合，自由エネルギーには2つの最小値が

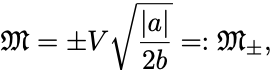
において存在する．
こちらは磁化が正負のどちらかに有限の値を持つことを意味するので強磁性相が対応する．

van der Waalsモデルのときと同様に

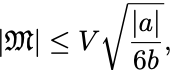
の領域では $F_M$ の $\mathfrak{M}$ についての2階微分が負になっており熱平衡状態が定義されない．
しかし

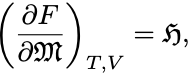
の関係から中間の状態を定められる．
温度 $T<T_c$ において外部磁場を正の側から$0$へ近づけることを考えると $H=0$ の直前の状態 $\mathcal{A}_*^{(1)}$ で自由エネルギーは微分可能でなければならない．
同様に負の側から $\mathfrak{H}=0$ に近づけた場合も同様に $\mathcal{A}^{(2)}_*$ で自由エネルギーは微分可能．
2つの状態 $\mathfrak{M}_{\pm}$ の間においても $\mathfrak{H}=0$ で一定だから，この中間領域において自由エネルギーは傾き $0$ の直線で結ばれる．
すなわち実際の自由エネルギーは $\mathfrak{M}_-\leq\mathfrak{M}\leq\mathfrak{M}_+$ において無限個の最小値を持つことになる．
印加する外部磁場を消したときこれらのうちどの熱平衡状態が実現されるかは預言できない（てこの規則のようなものがない）．

現実においてたとえば鉄を考えよう．
鉄は磁石になるが同じ温度でも磁石としてふるまうものとそうでないものがある．
磁石にならないのは異なる向きにそろった領域が複数混在し磁性を打ち消しあっているからである．
このような自発磁化が生じている領域を磁区といい，異なる磁区の境界を磁壁という．
一般の連続転移の文脈においてはそれぞれドメイン (domain)，ドメインウォール (domain wall) という．

一次元の場合は磁区は正負の2種類あり，どちらの向きにせよ自由エネルギーは偶函数なので寄与は同じである．
ただ磁壁の寄与が懸念されるが，磁壁の空間次元は系の次元より低い（厚さが十分薄い）とみなせるのでエネルギーの寄与も小さい．

以上から係数 $a$ の符号によって強磁性相と常磁性相の間の相転移が制御されている．
そこで相転移温度を $T_c$ とおいて

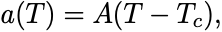
という形に仮定する．
このとき

とまとめられる．
系の対称性に着目して自由エネルギー（状態方程式）を仮定し連続な相転移を記述する方法をLandau理論という．

温度を固定して外部磁場を変化させたときの状態方程式 $\mathfrak{H}=\mathfrak{H}(T,V,\mathfrak{M})$ ． $\mathfrak{H}=0$ のとき青線で囲まれた領域のどこの状態が実現するかは予言できない．

温度を固定して外部磁場を変化させたときの状態方程式 $\mathfrak{H}=\mathfrak{H}(T,V,\mathfrak{M})$ ． $\mathfrak{H}=0$ のとき青線で囲まれた領域のどこの状態が実現するかは予言できない．

他方で温度を転移温度以下に固定して外部磁場を正の値から下げていくと磁化は減少し $\mathfrak{H}=0$ において $\mathfrak{M}_+$ に達しそのあと磁区に分かれたどこかの中間状態へ遷移する．外部磁場が負の値になると負の方向に磁化 $\mathfrak{M}_-$ が生じるようになる．
こちらは磁化の不連続な変化を伴う一次転移である．
転移温度以上では不連続転移はなくなる．
たとえば液相が負の磁化が生じている相，気相が正の磁化が生じている相となる．
そして気相と液相の区別がなくなる臨界点がCurie点に対応する．
気相と液相の共存状態が強磁性相に対応するが常磁性相に対応するものはない．