Prerequisite
ここまでで状態と物理量の概念の定式化をしてきた.
あとは実際に観測される物理量の測定値とその確率分布の定式化が必要である.
まず固有値が物理量の測定値に対応するということを仮定しよう.
つまり が成り立つ固有状態においては物理量
の測定値は
であると解釈する.
一般の状態ベクトルでは固有ベクトルの線型結合で表されるので,そこにおける物理量の測定値にはさらなる仮定が必要である.
まずオブザーバブル と正規直交完全系
を用意しよう.
この正規直交完全系で張られる状態空間の任意の元は,
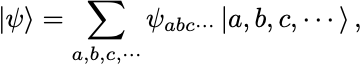
と書ける.
この に
を作用させてみると,

となる.
さらに左から を作用させると,
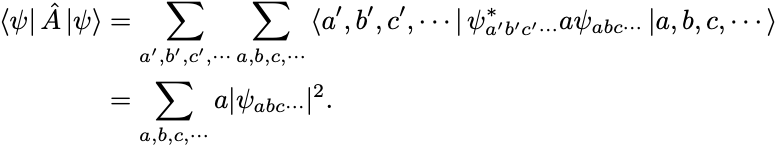
最後に両辺を で割ると,
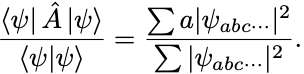
左辺をみると という重みのついた
の平均値あるいは期待値のような形をしていることに気づく.
そして は正規直交完全系で展開したときの
の成分なので状態ベクトルが各固有ベクトルの相対的な割合を示す量である.
そうしたことからこの が大きいほど対応する固有状態が実現されやすいという解釈が可能である.
そうして観測されるときにはそのどれかの の値が重み
で測定されるのである.
系の状態とは物理量のリストと確率分布である.
この定義では状態ベクトルと状態は一対一対応とは限らないことに注意する.
たとえば とスカラー倍した
は固有ベクトルの相対的な重みは同じである.
このことから2つの状態ベクトルに対してはベクトルとして等しいとするよりも,対応する状態が等しいとして状態ベクトルの同値性を定義する方が便利である.
そこで量子論では状態ベクトルの大きさを規格化 (normilization) して,定数倍の任意性を除いておくのが普通である.
すなわち全ての状態ベクトルに対して規格化条件,
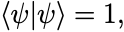
を課しておく.
これは定数倍したものは全て同値として大きさ の状態ベクトルを代表元にとってきたことと同じである.
ただしいま複素数体 上で議論しているので,大きさが定まってもまだ絶対値
の複素数倍だけの任意性が残る.
これを位相因子 (phase factor) といい一般に とかかれる.
そして位相因子だけ異なる状態ベクトルを集めた集合 は射線という.
後に述べるようにこの位相因子が直接物理的な意味を持つことはないのでふだんは としてかまわない.
規格化されれば
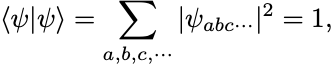
となって を確率分布と解釈することができる.
は状態に対して物理量
を測定したとき
が得られる確率を与える.
他の物理量 についても同様.
この確率分布を用いて物理量 の期待値は
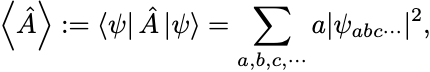
で計算できる.
註)ふつうの確率では を確率変数
の標本空間として

を満たすものであった.
また確率変数の函数 の期待値は
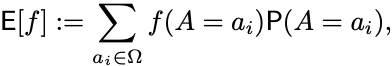
で計算される.
射影演算子 を用いれば
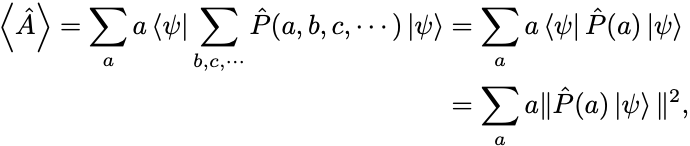
などと書くこともできる.
以上のことをまとめて次の仮定に集約する:
Bornの確率規則
状態 における物理量の確率分布は
で与えられる.
これをBornの確率規則という.
物理量の期待値まわりの分散は
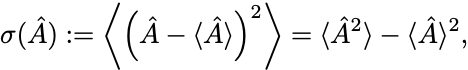
で定義される.
物理では平方根をとったゆらぎ をよく用いる.
これは古典確率と区別するために量子ゆらぎ (quantum fluctuation) とよばれる.
次節では量子ゆらぎの性質について議論する.
