Prerequisite
ここまでの古典的な議論でわれわれは粒子の位置や運動量を であるとか
であるとか仮定し議論してきた.
本来この値たちを知るためには観測者が観測をおこなわなければならない.
観測者という存在は理想的な存在であり,同時刻にあらゆる物理量を厳密に測定できると暗に仮定してきた.
しかしながら量子論においては本質的にゆらぎを含むので厳密な測定値を必ずしも与えられない.
粒子の座標や運動量を測定したければ試行回数を増やしてその平均値から推定するしかない.
観測という行為は観測者が対象の物理量の定まった1つの値を得る行為である.
このとき初めて粒子の物理量の値が確定するという立場が量子論である.
粒子がこれこれの物理量を持っていて観測するとたしかにその値が得られるという古典的な描像とは大きく異なる.
古典論で1粒子系を考えると初期条件として位置・運動量を与えると運動方程式からその後の時間発展を与えることができる.
他方で量子論では電子の位置・運動量を与えても(ある瞬間に位置・運動量を測定するということ),その後の時間発展は確率分布でしかわからないので,その後の物理量の値はふたたび測定しない限り確定していない.
しかし前述したように量子論では確率分布は確定する.
そして量子論では物理量・測定値・系の状態を分離してとらえることにする.
古典論ではたとえば位相空間上の1点で表されたように,系の状態は各粒子の物理量の定まっていてこれら3つの概念は同じものを指していた.
分離された3つの概念を定式化していこう.
われわれはまず系の状態を定式化するために次の仮定をおく:
状態ベクトル
系の状態はベクトル に対応する.
これを状態ベクトルという.
状態ベクトルの表記を太字ではなく上記のように表したのはふつうのベクトルとの違いを明確にするためであるのと,すぐ後で内積を定義するとき記号として使いやすいからである.
括弧の中身はベクトルを区別するためのラベルが入る.
量子論における系の状態とは,その系を特徴付ける物理量のリストとそれらの確率分布を指す.
今は状態ベクトルを抽象的な数学的対象と思って議論をすすめ,これらの情報が込められていることを後々見ていく.
ベクトル空間の定義をここでの表記を用いて復習しておこう.
ある集合 が体
上のベクトル空間 (vector space) であるとは,任意の元
と
に対して加法とスカラー倍,

が定義されて,次の公理を全て満たすようなもののことである:
-
: 加法の結合則
-
: 加法の交換則
-
: 加法の単位元の存在
-
: 加法の逆元の存在
-
: 加法とスカラー倍の分配則
-
:
上の加法とスカラー倍の分配則
-
: スカラー倍と
上の乗法の関係
-
: スカラー倍の単位元の存在
ベクトル空間の元をベクトル (vector) という.
註)加法の単位元を と表記したことに注意せよ.
慣習的に とは表記せず,この記号は別の状態に対応させる.
状態ベクトルの属するベクトル空間の次元については系によって様々であるので特に制限はない.
実際その次元は系によって有限であったり無限であったりする.
状態ベクトルは複素数 上で定義されている.
状態ベクトルの属する 上のベクトル空間を
とかく.
定義から状態ベクトルは次の性質を持つことがわかる: 任意の2つの状態ベクトル と
の線型結合,
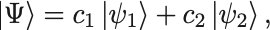
はふたたび状態ベクトルである.
ここに である.
状態を重ね合わせたものも状態ベクトルということは,対応する系の別の状態が存在することを示している.
これを状態ベクトルに関する重ね合わせの原理 (the principle of superposition) という.
次に状態ベクトルの内積を定義しよう.
内積の定義は函数 であって,
-
: 線型性
-
: Hermite対称性
,等号成立は
のみ: 正定値性
を満たすものとする.
この内積を,

とかく.
この記法を用いて上の定義を書き換えると,
-
: 線型性
-
: Hermite対称性
-
,等号成立は
のみ: 正定値性
となる.
定義の と
から左側の変数についても線型性,
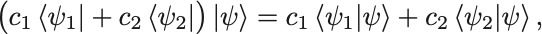
が成り立つことがわかる.
このような性質をHermite半双線型性という.
内積は二変数函数であるが,左側のベクトルを固定してみるとこれは右側のベクトルに関する1変数函数 となる.
この の内積で定義された函数全体の集合
を考えよう.
線型性より には自然に和とスカラー倍が定義され線型である.
よって がベクトル空間であることを示すのは
の内積の定義を用いればたやすい.
この を双対ベクトル空間という.
の元は
の元と,

という一対一対応がある.
その対応を

とかくことにしよう. の元
をケットベクトル (ketvector) といい
の元
をブラベクトル (bravector) という.
またそれらからつくられる複素数 のことをブラケット (bracket) という.
註)特殊相対性理論との関連で言えば,ケットベクトル が反変ベクトル
,ブラベクトル
が共変ベクトル
に対応している.
ブラケット は縮約をとる操作
に対応する.
ケットベクトルとブラベクトルには一対一対応があるからどちらも同じ状態に対応する状態ベクトルである.
Hermite対称性により

が成り立つ.
状態ベクトルの大きさを内積を援用して
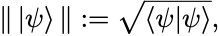
と定義できる.
平方根をとれるのは内積の正定値性から保証されている.
状態ベクトルの数学的準備ができたので,次の節では物理量の定式化を行う.
Problems
Cauchy–Schwarz不等式: 任意の状態ベクトルの内積に関して次の不等式が成り立つことを示せ:
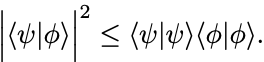
また等号成立条件を調べよ.
任意の複素数 と任意の2つの状態ベクトル
に関して,内積の正定値性から次が成り立つ:

複素数は2つの実数で の形に表せるので,

これは実数 に関する二次不等式である.
不等式が任意の に対して成立するためには判別式が
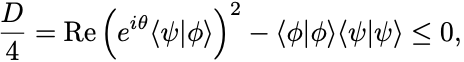
を満たさなければならない.
第1項を実数にするために として
となるように選ぶ(絶対値を
にするために
で割っていることに注意).
すると所期の不等式を得ることができる.
等号成立は2つのベクトルが「平行」なとき,すなわちある複素数 によって
と書けるときである.
三角不等式: 任意の状態ベクトルに関して次の不等式が成り立つことを示せ:

また等号成立条件を調べよ.
左辺の2乗を計算すると
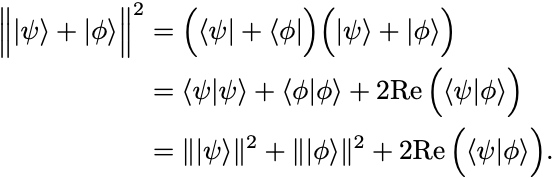
任意の複素数 について
なので
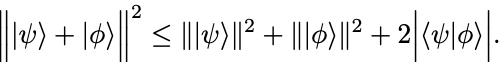
最後に前問のCauchy–Schwarzの不等式により,
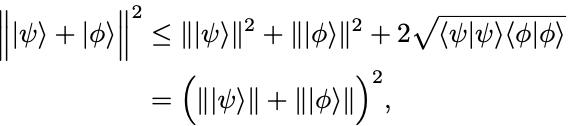
となって三角不等式が示された.
