三次元自由粒子の球面波解

~ QuantumAtsuo

Prerequisite

中心力場の最初の問題として，最も簡単な自由粒子 V=0 を考えよう．
直交座標での自由粒子の波動函数はすでに定常状態の章で議論した．
動径波動函数に関する方程式は

ここで \epsilon=2mE/\hbar^2 であるが自由粒子の場合は束縛状態はないので離散ラベル n は付けない．
境界条件は原点での条件が適用できる．
k=\sqrt{\epsilon} とおいて変数の無次元化 \xi=kr を行うと，

となる．この形の微分方程式は球Bessel微分方程式と呼ばれている．

この微分方程式の解は球Bessel函数と球Neumann函数があり，それぞれ

と定義される（解の導出は問題参照）．
これら2つの独立な解のうち球Bessel函数だけが原点で正則なので R_{kl}(r)=j_l(kr) となる．
よって自由粒子の（固有）波動函数は

である．
k は波動函数を定める連続なラベルであり，今考えているのが束縛状態ではないことに対応している．
一般解はさまざまなラベル k,\,l,\,m の函数の重ね合わせである.

球Bessel函数の概形

ここで球Bessel函数と球Neumann函数について触れておこう．
l の小さい方からいくつか具体的な函数形を与えておくと

原点 \xi\to0 においては

反対に無限遠 \xi\to\infty では漸近的に

また球Bessel函数はBessel函数 J_l(\xi) と次の関係にある：

Problems

\textsc{Problem1.}

次の漸化式が成り立つことを示し，これを利用して球Bessel微分方程式を解け：

\textsc{Solution.}

まず示したい漸化式の両辺に \xi^{-l-1} をかけることで

と変形して簡単化しておく．
球Beesel微分方程式を R_l から \chi_l に書き換えると

となる．
この両辺に (1/\xi)\mathrm{d}/\mathrm{d} \xi を作用させると

微分演算子と 1/\xi の交換関係を調べると

がわかる．
ここでの等号は微分演算子としてであることに注意せよ．
これらから微分方程式は

となる．
角括弧内の微分演算子は \chi_{l+1}(\xi) が満たす微分方程式のものと同じである．
全体の因子は規格化条件から一意に決まるので所期の漸化式を得る．

漸化式を繰り返し用いれば

あとは R_0(\xi) を求めれば良い．
l=0 のとき球Beesel微分方程式は

よって函数 \xi R_0(\xi) は三角函数の線型結合で書かれる．
正弦函数，余弦函数のそれぞれの解で

とおけば任意の l での球Bessel函数と球Neumann函数が得られる．

ちなみに独立な解として三角函数の代わりに指数函数 e^{i\xi},\,e^{-i\xi} に選ぶこともできる．
この選び方をした場合に得られる解，

をそれぞれ第一種・第二種の球Hankel函数という．

\textsc{Problem2.}

球Bessel函数と球Neumann函数の冪級数展開が展開が次のようになることを示せ：

\textsc{Solution.}

まずは球Bessel函数について見ていくと，三角函数をTaylor展開して

3行目へは微分演算子 \xi^{-1}\mathrm{d}/\mathrm{d} \xi を1つ作用させた．
このとき定数項（ n=0 ）は落ちるので和は n=1 からに変わる．
最後の表式に現れる1つ飛ばしの階乗について

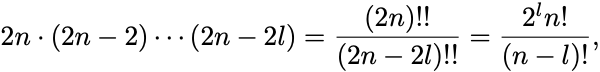
と変形できる．
また和のとり始めを n=0 にずらせば

を得る．

次に球Neumann函数は

球Neumannの場合は前から l 項目までについては注意が必要である．
0\leq n \leq l として

を調べよう．

となって負冪に達する．
この表式は n=l で適用できないが (2l-2n)!! を分母分子にかけることで

と変形すれば n=l にも適用できる．

n\geq l+1 ではその心配はなく

以上から

を得る．

\textsc{Problem3.}

球Bessel函数と球Neumann函数の \xi\to0,\,\infty での漸近形をそれぞれ求めよ．

\textsc{Solution.}

\xi\to0 で寄与が最も大きいのは冪級数の初項 n=0 である．
したがって前問の結果を眺めれば

がわかる．

次に \xi\to\infty のときの漸近形を求める．
球Bessel函数と球Neumann函数の具体形から分かる通り全ての項は \sin\xi\times\xi^{-k} または \cos\xi\times\xi^{-k} のような形をしている．
無限遠で支配的になるのはこの負冪が最も小さい項である．
球Bessel微分方程式の解の形から明らかなように，そのような項は微分演算子 \mathrm{d}^l/\mathrm{d}\xi^l が全て三角函数に作用した項

である．
（微分が 1/\xi に作用するとその分だけ負冪が下がっていく）
微分を評価するために指数函数を用いて

虚数と -1 を全て指数函数で書き表せば，

コメントを残す