この節ではベクトルを含む微分について簡単に述べておこう.
ベクトル場 をある軌道に沿って,軌道
のパラメータ
(たとえば時間)で微分すると鎖法則により
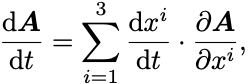
となる.
すなわち微分した結果はやはりベクトル場になっている.
次にベクトル場のベクトル変数 による微分を論じよう.
われわれがここまで扱ってきたのは 空間の
座標系である.
スカラー場の全微分 は

としてうまく定義することができた.
ベクトル場 の(全)微分を定義したいと思うのが自然である.
そのための方法の一つに微分形式という美しい理論を持ち出すことがある.
しかしこちらは一般性が高く抽象的なので後述することにして, 空間の直交座標に限定してもっと具体的な方法から出発しよう.
2つのベクトルに対する演算には,ベクトルへの写像である外積と,スカラーへの写像である内積があった.
それに対応してベクトルの微分にも2種類ある.

ベクトル場の例としてはたとえば風がある.
風は風向と風速が各点に定められている.
風は空気の流れである.
空気が地表面の全体でどのような密度分布で流れているかを調べたいことがある.
低気圧があるとその中心へ向かって風が吹き込み,高気圧があると中心から風が吹き出していく.
空間内にある有限の領域を考えてその境界を貫くベクトルの外向き成分の総量を調べれば,その領域がどれだけ放出しているのかあるいは吸引しているのかがわかる.
低気圧を囲む領域では内向きのベクトルが優勢であり,それらの合計は負のスカラー値になる.
各点に微小な領域を考えてこの量を定義したものが発散である.
次に低気圧・高気圧では風が渦を巻いている.
この向きの風,すなわち回転は発散を一切持たないようなベクトル場である.
発散は外向きベクトルの量であったからスカラー量であるが,回転は回転軸を持つためにベクトル量である.
任意の曲面を考えてその境界での境界に沿う向きのベクトル場を足しあげたときに,回転していればこれは値をもつ.
各点に微小な領域を考えてこの量を定義したものがベクトル場の回転である.
[発散]
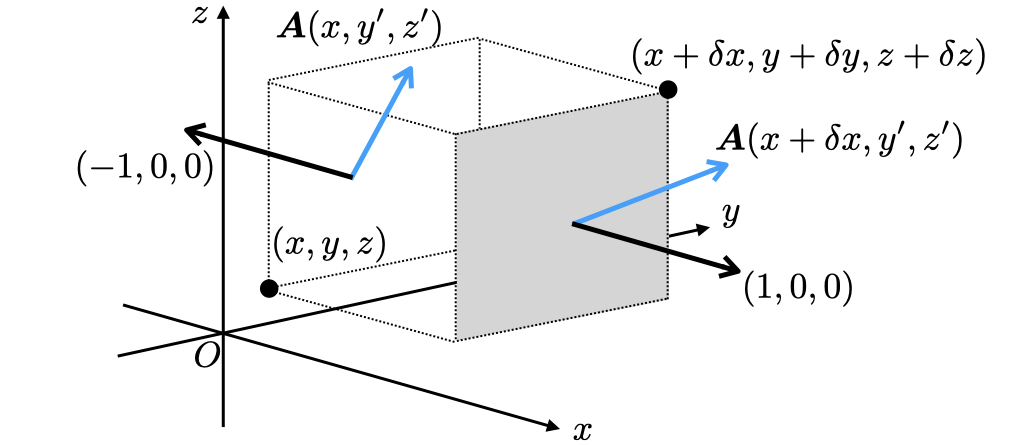
位置 にある微小な直方体
を考えよう.
各辺の長さを とすると体積は
となる.
この直方体の面に向きをつけて,この直方体から見て外向きを正とする法線ベクトルによって定める.
法線ベクトルも空間の各点で定義されるベクトル場である.
直方体は6面あって全て向きが違うので法線ベクトル6つによって向きがつけられる.
この直方体の向かい合うの2つの面に注目しよう.
まず で一定の面と
で一定の二面について見る.
法線ベクトルの成分はそれぞれ と
である.
この面上でベクトル場の値は と
をとる.
ただし である.
この微小体積から出て行く方向のベクトルの総量はそれぞれの法線ベクトルとの内積をとって

である.
面積 は微小面の総量にするためにかけている.
は微小なので1次までTaylor展開して,
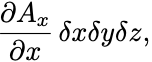
となる.
他の対面についても同様にして,

が得られる.
これら3つの和が微小体積 から放出する方向のベクトルの成分の総量である.
微小体積での値を各点の値にするには で割って平均化しておいて,最後に
とすればよい.
よって

これをベクトル場 の発散 (divergence) という.
真ん中の式の は微小直方体の表面にわたる総和を意味するものとし
はその微小な表面積.
発散は微分演算子 とベクトル場
の内積と一致している.
発散は と表記されることもある.
もし考えている領域 が有限の大きさをもっていて形も任意であったとしても,その領域を区分求積法のように微小な直方体に分割して各直方体上で今の議論を適用する.
そうすると内部の隣り合う直方体が共有している面に関して,同じベクトル場でもその法線ベクトルの符号が異なるために足し算でキャンセルされてしまう.
こうして 内の全ての直方体の表面でベクトル場の外向き成分を足しあげると結局
の境界
でのベクトル場の外向き成分だけが残ってくる.
外向き成分はベクトル場と境界面の法線ベクトル場 の内積で与えられる.
以上をまとめると

が成立する.
左辺の は体積
にわたる和であり,右辺の
はその境界
にわたる和を意味する.
(
)の極限で次の定理が得られる:
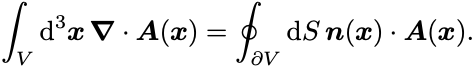
これをGaussの定理という.
Gaussの定理は体積積分をその積分範囲の境界上の面積分に還元する公式として非常に有用である.
[回転]

位置 にある
平面に平行で微小な長方形
を考える.
各辺の長さを とする.
軸について右回り(反時計回り)の向きを正と決めて,長方形を右回りにたどる経路とみなす.
たとえば長方形の左下の頂点 から右下
までで境界に沿ったベクトル場
の成分の和は
軸方向の線積分により,
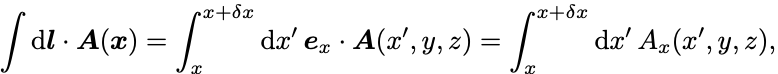
と書ける. の極限では高次の微小量を無視できて

となる.
他の辺でも同様にして長方形の境界に沿ったベクトル場 の成分の和は,

である.
さらに を微小量と思ってTaylor展開して整理すれば
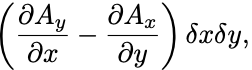
となる.
これが微小な長方形の 軸回りの回転を表す量である.
各点の値にするには面積 で割って平均化しておいて,最後に
とすればよい.
よって

が回転の定義となる.
真ん中の は
平面上の微小長方形の境界に沿った総和を意味するものとする.
また は経路に沿った方向ベクトルで大きさは微小.
他の軸の回りの回転も同様に計算できて,ベクトル量
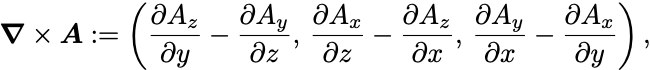
を定義できる.
これをベクトル場 の回転 (rotation) という.
回転は や
と表記されることもある.
また回転は微分演算子 とベクトル場との外積に一致しているので各成分はLevi-Civita記号を用いて
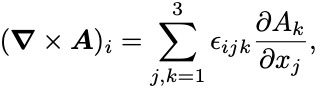
とも書くことができる.
有限の広さをもっていて任意のなめらかな曲面 に対しても,曲面を微小な長方形に分割することでその各々で同じ議論が可能となる.
この微小長方形はそれぞれ異なる法線ベクトル を持つ.
方向の軸周りの回転を計算するには,適当な回転変換によって
が
軸と平行になるようにする.
そこで長方形に沿ったベクトル場の線積分は上記と同様の計算のことから, 軸周りでは
成分だけなので

が得られる.
この表式は2つのベクトルの内積なので回転変換によって不変である.
したがって任意の の方向の軸回りでの回転は
で与えられる.
隣り合う長方形が共有している辺に関しては発散のとき同様に,経路の方向 が反対になるため足しあげたときキャンセルする.
したがって 内の全ての長方形の周でベクトル場の右回り成分を足しあげると
の境界
上を右回りにたどる経路上のベクトル場の線積分だけが残ってくる.
以上をまとめると
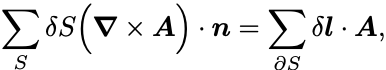
が成立する.
左辺の は曲面
にわたる和であり,右辺の
はその境界
に沿った和を意味する.
(
)の極限で次の定理が得られる:

これをStokesの定理という.
Stokesの定理は面積分をその積分範囲の境界に沿った線積分に還元する公式として非常に有用である.
最後に発散と回転の計算例を挙げておこう.
簡単なベクトル場 (
は定数)の場合,
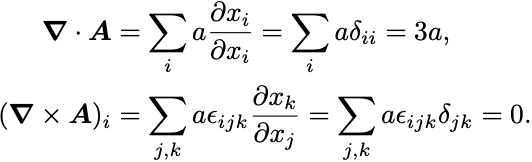
発散の計算ではKroneckerのデルタのトレースについて であることを用いた.
また回転の計算では対称テンソルと反対称テンソルの縮約が になることを用いた.
(
は定ベクトル)の場合は,

回転の計算の2行目へはLevi-Civita記号の縮約に関する公式を適用した.
のみの函数
については,

となる.
これらは簡単な微分の鎖法則によって

となることから導かれる.
