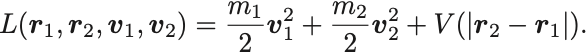Prerequisite
前節では慣性系における質点のLagrangianを導出した.
ここではポテンシャル があるときの質点系のLagrangianについて議論しよう.
結論から言ってしまえばそれは,
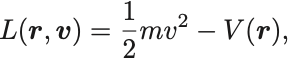
である.Euler–Lagrange方程式は,

となり,ふつうのNewton方程式に一致する.
変数変換 により一般化座標系へいつでも移ることができて,
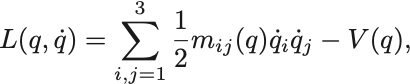
と書くことができる.ただし
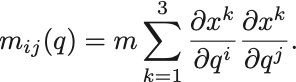
(このLagrangianに対するEuler-Lagrange方程式は節末の問題を参照せよ)
三次元直交座標 での
質点系のLagrangianを具体的に書くと,
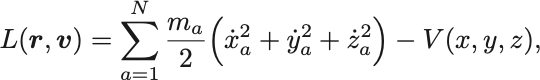
となる.円筒座標 へ移ると,
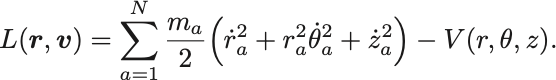
球面極座標 では,
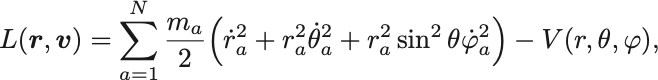
となる.円筒座標,球面極座標では速度(座標の時間微分)の2乗の項の係数は座標の函数であることに注意せよ.
Lagrangianの決定の問題にはいくつかの前提が必要である.
なぜポテンシャルを後ろに足すだけで良いのか,という問いにここまでの理論だけでは答えることができない.
Newton力学の結果と合うようにするにはそのような形が正しいのである.
またポテンシャルがもっと一般の函数 であってもこの仮定で正しい結果を与える.
Lagrangianを決定するための一般規則のようなものは存在しないが,対称性の議論からある程度制限をつけられる.
たとえばポテンシャルが付け加わるとGalilei対称性は一般に破れてしまう.
しかし後で詳細を議論するが,時空の並進対称性や回転対称性をもつことはでき,各々の対称性には保存則が対応することを見る.
もし系が明らかにエネルギーが保存している場合や運動量が保存している場合には,「Lagrangianがその保存則に対応した対称性をもつべき」という制限が加わる.
また時間反転の対称性や空間反転の対称性を明らかに持つ場合も同様である.
特殊相対性理論では「すべてのLagrangianがLorentz対称性をもたなければならない」という制限が加わる.
一般相対性理論では「すべての正則な座標変換に対して対称でなければならない」制限が加わる.
特殊相対性理論と量子論を統合した場の量子論では,LagrangianはLorentz対称性と時空の並進対称性をもつべきであり,さらにゲージ対称性とくりこみ条件が課される.
この2つによって粒子間の相互作用の形が決定される.
くりこみは計算手法の1つである.この計算手法が破綻しないための条件がLagrangianに課されるのである.
以上は素粒子論に基づくLagarangianの構成の仕方であるが,このような考え方は統計力学や物性理論においても有用である.
後の節で解析力学における対称性の重要性について議論していこう.
Problems
次のLagrangianについてEuler–Lagrange方程式を導出せよ.
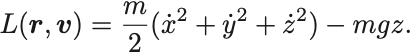
ただし は正の定数.
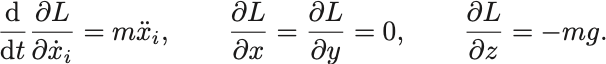
これらを合わせて,

を得る.これらは 軸の負の向きに一様重力場がはたらくときの質点の運動方程式に一致している.
次のLagrangianについてEuler–Lagrange方程式を導出せよ.
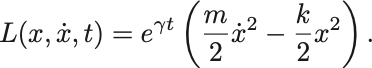
ただし は正の定数.
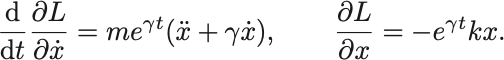
これらを合わせて,

ただし .左辺の丸括弧の中は減衰振動の運動方程式に一致している.
次のLagrangianについてEuler–Lagrange方程式を導出せよ.
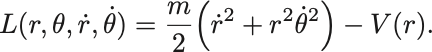
ただし は正の定数.
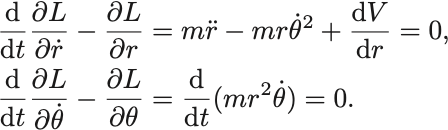
2つ目の運動方程式は,角運動量保存則に対応しており, が保存量であることがわかる.
を用いて1つ目の式から
を消去すると,

を得る.これは中心力場中での軌道を決める運動方程式に一致している.
相互作用項は相対座標 を用いて
とかける.
運動項については,
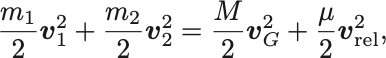
と分離できる.ここで は全質量,
は換算質量,
は重心速度である.
よって重心座標 と相対座標
を基本変数とするLagrangianは,
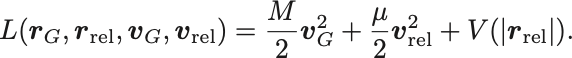
Euler–Lagrange方程式は,
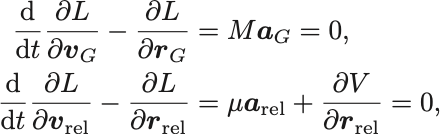
となる.ただし ,
.
次の一般化座標におけるLagrangianに関するEuler–Lagrange方程式を導出せよ.
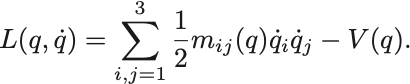
ただし は正定値.
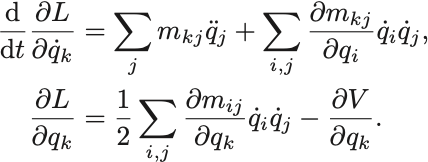
これらを合わせて,
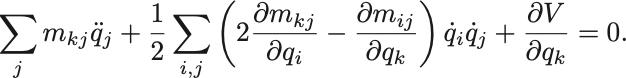
ここで
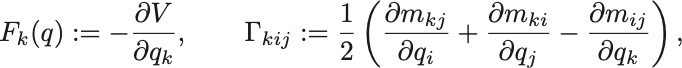
とおくとEuler–Lagrange方程式は

となる. は一般化力,
はChristoffel記号という.