電磁波の性質

Prerequisite

電磁波

この節では前節で求めた輻射ゲージの波動方程式の解

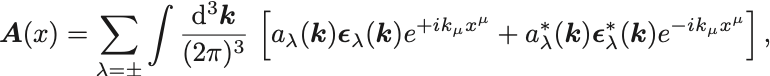
の性質を調べていく．
電場と磁場は

で計算できる．

四元ポテシャンルが波数ベクトルを1つ $\boldsymbol{k}_0$ のみを含む場合を考えよう．
これは一般解で

とおいたときの解に対応していて

単色平面波

ここで $k_0^{\mu}=(\omega_{\boldsymbol{k}_0}/c,\,\boldsymbol{k}_0)$ ，

とおいた．
この解を単色平面波解 (monochromatic plane wave) という．

単色平面波の電場と磁場は

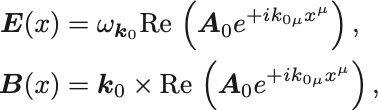
と計算される．
2式を比べれば電場と磁場の間には

の関係があることがわかる．
ここで $\boldsymbol{n}_0=\boldsymbol{k}_0/|\boldsymbol{k}_0|$ は波数ベクトルと平行な方向ベクトル．
電場は偏極ベクトルの線型結合で書かれているから波数ベクトル $\boldsymbol{k}$ と直交している．
これは電荷のないところでのGaussの法則 $\boldsymbol{\nabla}\cdot\boldsymbol{E}=0$ からもわかる．
また磁場は電場と波数ベクトルの外積で書かれているのでこれら2つの方向とも直交している．
これはFaradayの法則 $\boldsymbol{\nabla}\times\boldsymbol{E}=-\dot{\boldsymbol{B}}$ からもわかる．
さらに電場と磁場は同位相で振動することもわかる．

単色平面波の電場を改めて

とおく．
複素ベクトル $\boldsymbol{E}_0$ は $\boldsymbol{k}$ と直交するので2つの実基本ベクトル $\boldsymbol{\epsilon}_1,\,\boldsymbol{\epsilon}_2$ で展開できて

ただし $E_{01},\,E_{02},\,\phi_1,\,\phi_2\in\mathbb{R}$ ．
これから

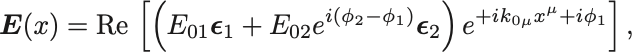
とできる．
位相因子 $e^{i\phi_1}$ は座標の取り方で落とせるので無視してもよい．

$\phi_1=\phi_2$ の場合，

となる．
ここで $\boldsymbol{E}_0=E_{01}\boldsymbol{\epsilon}_1 + E_{02}\boldsymbol{\epsilon}_2$ と定義し直した．
この場合，電場は $\boldsymbol{k}$ に直交した一定の方向 $\boldsymbol{E}_0$ を向いて振動することがわかる．
これを直線偏光 (linear polarization) という．
磁場も同様である．

$\phi_1\neq\phi_2$ の場合は，

$\boldsymbol{E}(x) = E_1\boldsymbol{\epsilon}_1 + E_2\boldsymbol{\epsilon}_2$ と係数をおけば

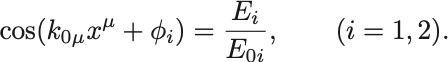
なので， $\phi_2-\phi_1=\delta$ とおいて，

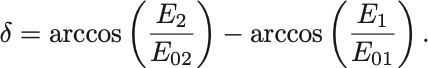
これから

が導かれる．
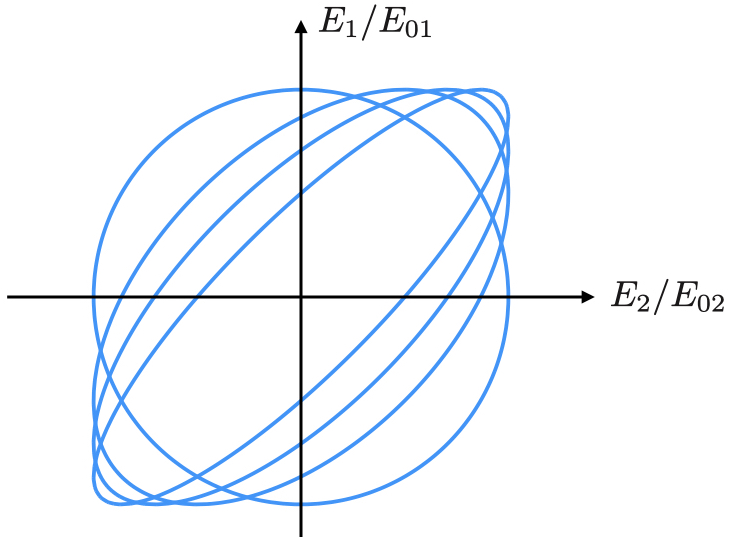
この式は電場が楕円を描くことを示し，この解を楕円偏光 (elliptic polarization) という．
特に $\delta = \pm\pi/2$ かつ $E_{01}=E_{02}=:E_0$ のときは円を描くので円偏光 (circular polarization) という．
円偏光のとき

円偏光のうち波数ベクトルの方向 $\boldsymbol{n}$ について右回りのものはヘリシティ (helicity) が負という．
また左回りのものはヘリシティが正という．

次に単色平面波のエネルギーを計算してみよう．
ここでは簡単にだけ計算する．
電磁場のエネルギーは

今 $\boldsymbol{B}=\boldsymbol{n}_0\times\boldsymbol{E}/c$ かつ $\boldsymbol{n}_0\cdot\boldsymbol{E}=0$ なので

となる．
よってエネルギー密度は電場だけで

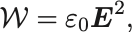
によって計算できる．

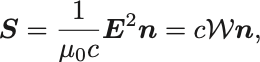
エネルギーの流密度を表すPoyntingベクトルは $\boldsymbol{S}=\boldsymbol{E}\times\boldsymbol{B}/\mu_0$ より

となる．
単色平面波のエネルギーの流れは波数ベクトルと平行であり，エネルギー密度を光速で伝搬していると解釈できる．
つまり電磁波は光速で伝搬することがわかる．
また電磁場の運動量密度は $\boldsymbol{S}/c^2$ なので単色平面波のエネルギーと運動量の関係は

となる．
これは質点のEinsteinの関係式 $E=\sqrt{|\boldsymbol{p}|^2c^2+m^2c^4}$ においてmassless； $m=0$ としたものと一致する．
すなわち電磁波がmassless粒子であることを示唆している．
実際場の量子論では光子と呼ばれる粒子の集団として電磁場を扱う．