Prerequisite

前節で求めたMaxwell方程式の特解を用いて運動する荷電粒子が作る電磁場を求めよう.
かなり煩雑な計算なのでうまく整理しながら進めていく.


荷電粒子の三次元の軌道を とする.
は荷電粒子の時刻で観測点の時刻
と区別する.
四元ベクトルでは とかける.
四元電流密度 は

で定義される.
ここで は軌道パラメータを時間
としたときの荷電粒子の四元速度.
四元電流密度にデルタ函数 を挟み込んで

さらに変数変換 によって軌道のパラメータを時間から任意のものに取り換えれば

となる.
四元速度 とおいた.
この四元電流密度と遅延Green函数を代入すれば

2つ目の等号ではデルタ函数をつかって を荷電粒子の軌道
で書き換えている.

次にもう一つのデルタ函数による積分を計算したい.
そのためにデルタ函数の公式

を用いる.
ここで は
の零点;
.
となるパラメータを
とおく.
さらに

とおくと

となるので, の条件はヌル
の1つの解と言える.
この条件は観測点 の光円錐の過去側と軌道の交点におけるパラメータを定めている.
遅延Green函数は観測点より過去側の光円錐上の物質の情報を足し上げていたが,荷電粒子の場合それは の1点の寄与のみである.
もう1つの解は先進ポテンシャルに対応していて,観測点 の光円錐の未来側と軌道の交点におけるパラメータ
を与える.
とりもなおさずデルタ函数の公式により

となる.
ここで表記の簡単のためと無次元化するために

とおいた.
絶対値を外すために の符号を評価しておく.
まずパラメータとして時間を選んで とすると
とかける.
であり,
であることから

なので が導かれる.
したがって,

以上から

パラメータとして時間を選んで とすると
に対する条件は
光円錐条件

となる.
スカラーポテンシャルとベクトルポテンシャルはそれぞれ,
Liénard–Wiechertポテンシャル

これらが荷電粒子がつくる電磁ポテンシャルでありLiénard–Wiechertポテンシャルという.
荷電粒子が静止している の場合,
かつ
となって静電場のCoulombの法則に一致する.
最後にLiénard–Wiechertポテンシャルから電場と磁場を計算しよう.
以下表記の簡単のため添字 を省略する.
電場と磁場を効率的に計算するために

という量を考える. を用いて電場,磁場はそれぞれ

で計算可能となる.
註) は電磁場テンソルと呼ばれ電磁気学において重要な量である.場の解析力学の章で詳しく触れる.
を計算するために場の引数
とそれを含む
があらわな式に書き換えると

微分は直接 に作用する部分と
を通して
に作用する部分とに別れるので

第1項については

と計算されるがこれは と
について対称なので
の計算で落ちる.
第2項についてはまず光円錐条件を微分して

について解いて整理すれば

を得る.
次に を計算していくと

となる.
ここで

とおいた.
以上から

の部分は
の計算で落ちる項を略記している.
よって

と求まる.
まず電場を に注意して直接計算すると
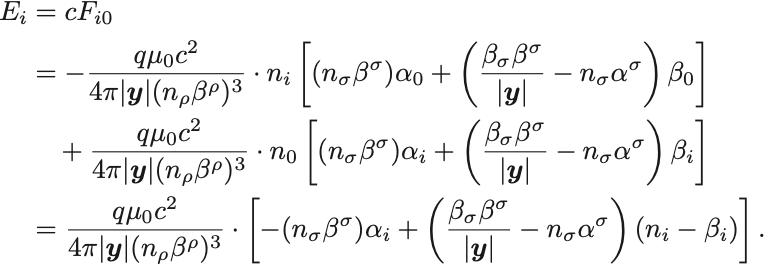
よって三次元のベクトル表記では
荷電粒子のつくる電場

一方磁場の方は次のように計算する:
まず が

とおけることに着目する.
そして

と変形する.
ここに を挟み込んで,さらに
であることを利用して
を加えれば

となって電場から磁場を計算することができる.
この節の結果をまとめておこう.
荷電粒子のつくる電磁ポテンシャルの特解はLiénard–Wiechertポテンシャル

でかかれる.
Liénard–Wiechertポテンシャルから導かれる電場と磁場は

ここで

