Prerequisite
この節では量子論における摂動 (perturbation) を扱う.
量子論でも考え方は同じで解がよくわかっている方程式からのわずかなずれ(摂動)を系統的に取り込む.
古典論では運動方程式の解は粒子の軌道で,摂動によるずれを調べた.
量子論ではSchrödinger方程式の解は状態ベクトルの時間発展である:
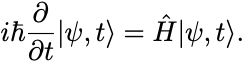
簡単のために定常状態に限定すれば対応するのは状態ベクトルとその属するエネルギー固有値

であり,それらの摂動による影響を調べれば良い.
Hamiltonian に摂動Hamiltonian
が付け加わったとする.
小さいことをあらわにするために微小なパラメータ を用いて,
とおく.
いまこの摂動 は時間に依らないとする.
時間による場合は次節以降で扱う.
もとのHamiltonianについては次の固有値方程式が成り立っていてその解は与えられているものとする:

状態ベクトルの後ろのラベル は摂動がない第0近似を意味する.
さらに今は縮退が存在せず ならば
であると仮定する.
摂動Hamiltonianが加わると固有状態も微小に変化をうけて新たに,

が成り立つとする.
摂動パラメータ で固有状態と固有値を展開(摂動展開)すると,
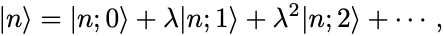

この2つの展開式を固有値方程式に代入すれば,

の冪ごとに整理すれば,
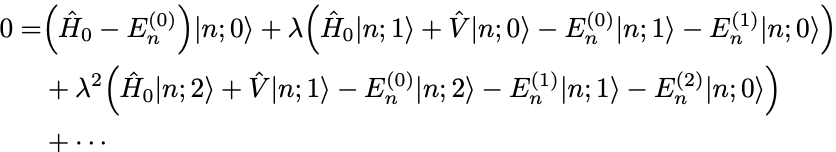
は任意に選べるから各冪がそれぞれ
に等しく,



などが成り立つ.
1番目は初めの摂動がないときの固有値方程式に他ならない.
2番目以降が摂動に関する方程式になっている.
2つ目の式の左から を作用させると,

整理して,

ここで

は摂動ポテンシャル の行列要素である.
とおくと左辺は
になるから,
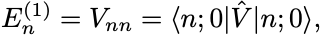
としてエネルギー固有値の1次の補正が得られる.
のとき
であり,

の完全性より
をこれらで展開できて,
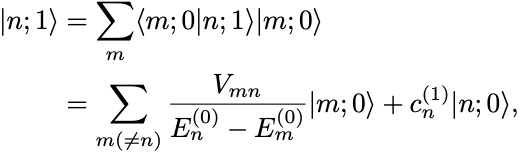
となる.
ここで であり未定の定数として残る.
これを除けば一次の摂動に関する状態ベクトルとエネルギーが求まり,固有状態たちとエネルギー固有値の の1次までの補正を与える.
つまり,


では同様にして2次の補正を求めよう.
今度は2次の式の左から を作用させると,

として整理すると,

1次の摂動に関してはすでにもとまっているのでその結果を代入すると第2項は 以外が直交性から落ちて,

となる.
2行目から3行目へは1次の摂動エネルギーの式を用いた.
次に の場合は
より,
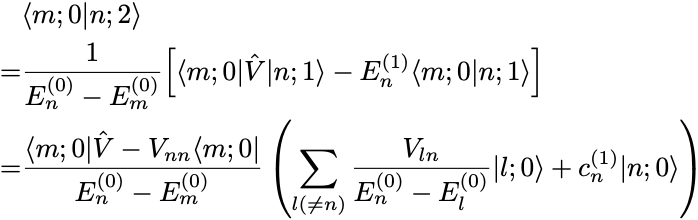
の直交性により,

以上から1次のときと同様に完全性より,

となる.
ただし .
摂動を受けた後の状態ベクトルの規格化を行おう.
1次までで状態ベクトルの大きさは,

となる.
よって任意の でこれが
に規格化されるためにはたとえば
に選べばよい.
2次までの摂動を取り入れたときの固有状態ベクトルは,不定係数の項を抜き出して

となっている.
ただし状態ベクトルの摂動補正の項は不定係数の項を抜き出して
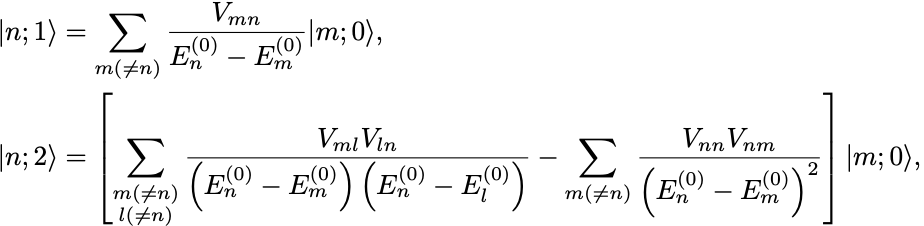
と定義し直した.
このとき特に となっている.
したがって不定係数は結局状態ベクトルの全体の係数に という形で現れるだけである.
これは状態ベクトルの定数倍の不定性をつかって をスケールすればいつでも取り除くことができる.
不定係数を取り除いた上でさらに,摂動を受けたあとの状態ベクトルが正しく規格化されためには適当にスケーリング をおこなって状態ベクトルを再定義する必要がある:
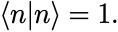
このときパラメータは

に選べば良い.
この操作を再規格化 (renormalization) あるいはくりこみという.
