時間に依らない摂動論; 射影演算子の方法

Prerequisite

この節では摂動のある定常Schrödinger方程式を解くための形式的な解法与える．
まずはエネルギー固有値に縮退がないと仮定しよう．
固有状態のラベルを $n$ として非摂動系において

が成り立っている．
$0$ は非摂動を明示するために付している．
摂動が加わった $\hat{H}=\hat{H}_0+\lambda\hat{V}$ における定常Schrödinger方程式を

とおく．

次に2つの射影演算子

を導入しよう．
$\hat{Q}_n$ は $n$ 番目の固有状態への射影で $\hat{P}_n$ はそれと直交する空間への射影である．
射影演算子は非摂動Hamiltonianと可換である； $[\hat{Q}_n,\hat{H}_0]=[\hat{P}_n,\hat{H}_0]=0$ ．
固有値方程式の左から $\hat{P}_n$ を作用させると，

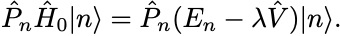
ここで任意のパラメータ $\Theta$ を導入して上式を

と変形する．
左辺では可換性から

となる．
逆演算子 $(\Theta-\hat{H}_0)^{-1}$ を左から作用させれば

を得る．
ここで射影演算子と非摂動Hamiltonianが可換なので形式的に分数の形で略記したが，厳密には $(\Theta-\hat{H}_0)^{-1}\hat{P}_n$ の意味である．
いまこの式の両辺には摂動を受けている系の固有状態 $|{n}\rangle$ が現れている．
これを右辺の $|{n}\rangle$ に代入することで，

となり再帰的に同じ式の代入をくり返していけば，

となる．
こうして摂動を受けている系の固有状態 $|{n}\rangle$ を $|{n;0}\rangle$ から求める式が得られた．
あとは具体的な $\Theta$ を与えれば逐次的に解くことができる．

エネルギー固有値を求めるには固有値方程式の左から $\langle{n;0}|$ を作用させることで

となるので， $E_n$ について解けば

状態ベクトルの形式解を代入すれば

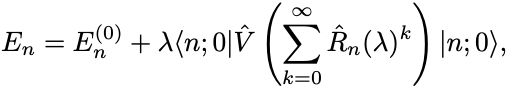
と与えられる．
摂動展開から求めた結果と一致していることを見るためには $\Theta=E_n^{(0)}$ とおけば容易く確かめられる（問題参照）．
この場合に得られる形式解はRayleigh–Schrödinger方程式という．
他方で $\Theta=E_n$ とする場合に得られる形式解はBrillouin–Wigner方程式という．
これらは摂動展開の収束性によって使い分けられる．

では次に縮退がある場合で同様の形式解を導いていこう．
縮退がある場合の非摂動固有状態は縮退のラベル $\alpha$ が加わって $|{n,\alpha;0}\rangle$ と書かれて，

と展開できる．
これらの固有状態ベクトルは

を満たす．
摂動を受けるとエネルギー固有値の縮退は一般に解けて $E_{n,\alpha}$ と表記される．
摂動のある系の定常Schrödinger方程式は

同様に $E_n^{(0)}$ に属する固有空間への射影演算子

を導入する．
定常Schrödinger方程式に任意パラメータ $\Theta$ を導入し左から $\hat{P}_n$ を作用させれば

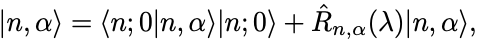
上式を逐次的に代入して

を得る．
エネルギー固有値については定常Schrödinger方程式の左から $\langle{n;0}|$ を作用させれば

と変形できる．
上の結果を代入すると

となり縮退のラベル $\alpha$ を除いて縮退がないときと全く同じ形で与えられる．

具的系に $\Theta=E_n^{(0)}$ として1次と2次の項を計算してみよう．
エネルギー固有値は $\hat{P}_n|{n;0}\rangle=0$ に注意して

$\lambda$ について1次，2次の項を $E_{n,\alpha}^{(1)},\,E_{n,\alpha}^{(2)}$ とおく．
1次の項については

$d_n\times d_n$ の正方行列 $\mathsf{V}_n=(\langle{n,\beta;0|\hat{V}\rangle|n,\gamma;0})$ と $d_n$ 次元のベクトル $\boldsymbol{c}_n^{(0)}=(c_{n,\beta}^{(0)})$ を導入すれば

と書かれる．
これは $|\boldsymbol{c}_n^{(0)}|^2=1$ のもとでの行列 $\mathsf{V}_n$ の固有値問題と等価である．固有ベクトルは $d_n$ 個あり，そのうち $E_{n,\alpha}$ に対応するものとして $\boldsymbol{c}_{n;\alpha}^{(0)}=(c_{n,\beta;\alpha}^{(0)})$ と表記しよう．
さらに記号が煩雑になってしまうがこの係数によって展開される非摂動の固有ベクトルを

と表記する．
つまりここまで出てきた $|{n;0}\rangle$ は $|{n;0_{\alpha}\rangle}$ に読み替える．

2次の項については完全系の式 $\hat{I}=\sum_m|{m;0}\rangle\langle{m;0}|$ を挿入して

となる．
射影演算子 $\hat{P}_n$ のために和から $n$ 番目が除去されることに注意せよ．
1次の摂動を取り入れてもまだ縮退が残っている場合は2次の摂動でそれが解けることがある．
1次で縮退が残ると展開係数 $c_{n,\beta;\alpha}^{(0)}$ が完全に定まらない．
そのとき再び2次のエネルギー補正 $E_n^{(2)}$ を固有値とするような固有値問題が立てられて展開係数を固有ベクトルとして定めることができる．