写像 – 物理とはずがたり

Prerequisite

集合

2つの集合 $A,B$ の要素の間に対応規則をつけることを考える．
その中でもすべての $a\in A$ に対して $B$ のいずれかの要素 $b\in B$ を対応づける規則のことを $A$ から $B$ への写像 (map) という．
特に数の集合から数の集合への写像は函数 (function) と呼ばれる．
$A$ から $B$ への写像を記号で $f\colon A\to B$ と書く．
また $a\in A$ が $b\in B$ に対応づけられていることを

と表記する．

写像に関するいくつかの概念を定義していこう．
写像 $f$ の対応先の全ての元からなる集合

を定義できる．
これを $f$ による $A$ の像 (image) という．
明らかに $f(A)\subseteq B$ である．
また $A$ の任意の部分集合 $A'\subseteq A$ に対してもその像 $f(A')$ を定義できる．

$B$ の任意の部分集合 $B'\subseteq B$ に対して

で定義される $A$ の部分集合を $B'$ の逆像 (inverse image) という．
特に $f^{-1}(B)=f^{-1}(f(A))=A$ である．

写像 $f\colon A\to B$ が任意の2つの元 $a_1,a_2\in A$ に対して

を満たすとき $f$ は単射 (injective) という．
つまり単射な写像は異なる元は異なる元に対応づけていて重複させることはない．
対偶をとった条件

も単射性の証明において便利である．

写像 $f\colon A\to B$ が任意の元 $b\in B$ に対してある $a\in A$ が存在して $b=f(a)$ と書けるとき $f$ は全射 (surjective) という．
つまり全射な写像は全ての元と全ての元が対応づけられていることを意味する．
それゆえ $f$ が全射ならばその像について $f(A)=B$ が成り立つ．

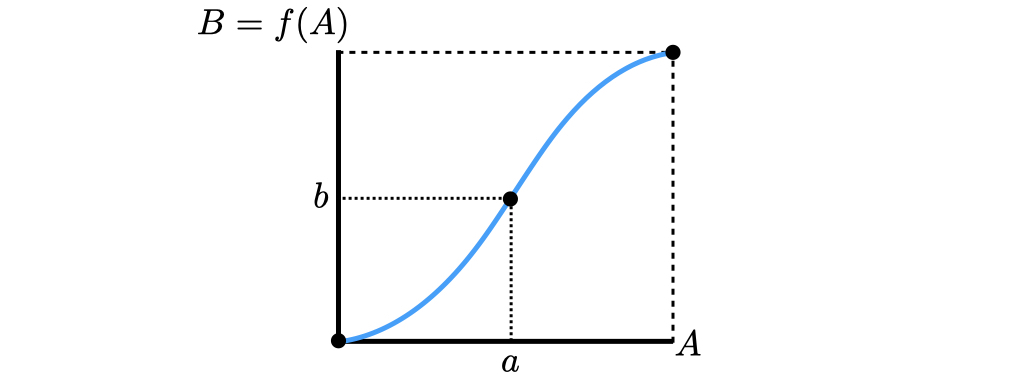
全射かつ単射な写像のことを全単射 (bijective) という．
全単射な写像ではお互いの元の全てが重複なく対応づけられることから1対1対応するともいう．

2つの写像 $f\colon A\to B$ と $g\colon A\to B$ について，もし任意の元 $a\in A$ の対して

が成り立つならばこの2つの写像は等しいとし $f=g$ と表記する．

任意の集合 $A$ に対し写像 $\iota\colon A\to A$ で任意の $a\in A$ に対してそれ自身 $i(a)=a\in A$ を対応づける写像が存在し，恒等写像 (identity map) という．
恒等写像は明らかに全単射である．

集合 $A,B$ の要素の個数を $n_A,n_B$ とする．
$n_A<n_B$ のとき必ず $n_B-n_A$ 個の $B$ の元が対応づけされず余ってしまうので全射は存在できない．
多方で $n_A>n_B$ のときは $n_A-n_B$ 個の $A$ の元の対応づけ先が不足しているので必ず重複が発生し，単射は存在できない．
$n_A=n_B$ のとき，重複なく対応づけして単射を構成すると必然的に全射となる．
つまりこのときは単射または全射であれば必ず全単射である．

集合の要素が有限個であればこのように写像の全射，単射は簡単である．
次に無限個の場合について考える．
一般には濃度と呼ばれる数学的概念を導入するがここでは省略する．

整数 $n\in\mathbb{Z}$ から $m\in\mathbb{Z}$ への写像として $f\colon n\mapsto m=2n$ を考える．
この写像は単に整数を二倍するので重複はなく単射である．
しかし像 $f(\mathbb{Z})$ は偶数の全体の集合なので任意の奇数には $m=f(n)$ となるような対応元の整数が存在しない．
ゆえに $f$ は全射ではない．

写像 $f\colon n\mapsto m=(-1)^{n-1}\lceil |n|/2\rceil$ は全射だが単射ではない例である（ $\lceil x\rceil$ は天井函数）．
なぜなら任意の $m\in \mathbb{Z}$ に対して $m\leq0$ ならば $n=\pm2m$ ， $m>0$ ならば $n=\pm(2m-1)$ が対応元として存在する．

写像 $f\colon n\mapsto m=(-1)^n$ は全射でも単射でもない．
像は $f(\mathbb{Z})={+1,-1}$ であり全ての偶数が $+1$ に対応して重複している．

次に実数から実数への函数 $f\colon\mathbb{R}\to\mathbb{R}$ についていくつか例を見ていこう．
まず $f\colon x\mapsto y=2x$ は整数のときと違って全単射である．
正弦函数 $f\colon x\mapsto y=\sin x$ は像が区間 $f(\mathbb{R})=[-1,1]$ であり $2\pi$ の周期で同じ値をとるので全射でも単射でもない（余弦も同様）．
多方で正接函数 $f\colon x\mapsto y=\tan x$ は $2\pi$ の周期があるので単射ではないが任意の実数値をとれるので全射である．
ただし正接函数は $\pm\pi/2+2n\pi$ で発散するので実数全体で定義される函数ではなく，厳密にはこれらの発散する点を除いた集合上で定義された函数である．

指数函数 $f\colon x\mapsto y=e^x$ は負の値をとれないので単射であるが全射ではない．

双曲線函数 $f\colon x\mapsto y=\sinh x$ は全単射である．
一方で $f\colon x\mapsto y=\cosh x$ は $1$ 未満の実数をとれないので全射ではないかつ $\pm x$ は同じ $\cosh x$ に対応するので単射でもない．

写像 $f\colon A\to B$ が全単射のとき次のようにして新たな写像 $g\colon B\to A$ を構成できる．
$f$ の全射性より任意の $b\in B$ に対して $a\in A$ が存在する．
これは一般に複数存在するが単射性よりただ1つに決まる．
そこで任意の $b\in B$ に対して $f(a)=b$ となる $a$ を対応づける写像として $g$ を定義できる．
この $g$ を逆写像 (inverse map) といい

と表記する．
また構成法より明らかに $f^{-1}$ は全単射である．

実数から実数への函数 $f\colon\mathbb{R}\to\mathbb{R}$ で逆写像の例を見ていく．
この場合逆写像は逆函数と呼ばれる．
$f\colon x\mapsto y=2x$ に対しては $f^{-1}\colon y\mapsto x=y/2$ が逆函数である．

正の実数全体の集合を $\mathbb{R}_{>0}$ とする．指数函数を $f\colon \mathbb{R}\to\mathbb{R}_{>0}$ と見ればこれは全単射であるから逆函数が存在できる．
実際，逆函数は対数函数であり $f^{-1}\colon y\mapsto x=\ln y$ と表される．

同様にして正弦函数を実数の区間から区間への写像 $f\colon [-\pi/2,\pi/2]\to [-1,1]$ と見れば全単射となる．
逆函数は逆正弦函数 $f^{-1}\colon y\mapsto x=\arcsin y$ である．

3つの集合 $A,B,C$ に対して2つの写像 $f\colon A\to B$ と $g\colon B\to C$ を考える．
任意の $a\in A$ を $f$ で移して $b=f(a)\in B$ となった後，さらに $g$ で移して $c=g(b)=g(f(a)) \in C$ とすることができる．
この対応づけによって新たな写像

が構成できる．
これを $f$ と $g$ の合成写像 (composition map) という．

4つの集合 $A,B,C,D$ に対して3つの写像 $f\colon A\to B$ と $g\colon B\to C$ ， $h\colon C\to D$ を考える．
このとき先に $f,g$ を合成した場合の合成写像 $h\circ(g\circ f)$ と $g,h$ を先に合成した場合の $(h\circ g)\circ f$ が考えられるが，任意の元 $a\in A$ に対して両方とも $h(g(f(a)))$ と対応づくことから写像として等しいことがわかる．
よって括弧を外して $h\circ g\circ f$ と表記する．

全単射な写像 $f$ には逆写像 $f^{-1}$ が存在する．
この2つの合成写像 $f^{-1}\circ f\colon A\to A$ と $f\circ f^{-1}\colon B\to B$ は恒等写像 $\iota$ に等しい．
任意の元 $a\in A$ に対して $b=f(a)\in B$ が存在し，逆写像の性質から任意の $b\in B$ に対して $b=f(a)$ となる $a\in A$ が対応づく．
よって $f^{-1}\circ f(a)=a=\iota(a)$ ．
このことは後で集合 $A$ の全単射全体の集合が群をなすことを意味しているのがわかる．

たとえば指数函数と対数函数ではたしかに任意の実数 $x\in\mathbb{R}$ に対し $\ln(e^x)=x$ と，任意の正の実数 $x\in\mathbb{R}_{>0}$ に対し $e^{\ln x}=x\in\mathbb{R}_{>0}$ が満たされている．

Problems

$\textsc{Problem. 1}$

集合 $A,B$ と写像 $f\colon A\to B$ を考える．
$A$ の部分集合 $A',\,A''\subseteq A$ について以下が成り立つことを示せ:

$A'\subseteq A''$ ならば $f(A')\subseteq f(A'')$ ．
$f(A'\cup A'')=f(A')\cup f(A'')$ ．
$f(A'\cap A'')\subseteq f(A')\cap f(A'')$ ．

$\textsc{Solution. }$

(i) 任意の $b\in f(A')$ に対しある $a\in A'$ があって $b=f(a)$ である．
$A'\subseteq A''$ なので $a\in A''$ であるから $b\in f(A'')$ が言える．

(ii) 定義より

2行目へは和集合の定義，3行目へは像の定義，4行目へは和集合の定義をそれぞれ適用した．

(iii) $A'\cap A''\subseteq A'$ より(i)を適用して $f(A'\cap A'')\subseteq f(A')$ ．
同様に $A'\cap A''\subseteq A''$ より $f(A'\cap A'')\subseteq f(A'')$ ．
任意の $b\in f(A'\cap A'')$ は部分集合の定義より $b\in f(A')$ かつ $b\in f(A'')$ である．
ゆえに積集合の定義より $b\in f(A')\cap f(A'')$ ． $\Box$

$\textsc{Problem. 2}$

集合 $A,B,C$ と2つの写像 $f\colon A\to B$ と $g\colon B\to C$ に対し以下が成り立つことを示せ:

$f,\,g$ が単射ならば $g\circ f$ は単射である．
$f,\,g$ が全射ならば $g\circ f$ は全射である．

$\textsc{Solution. }$

(i) $f,g$ を単射とする．
$g\circ f(a_1)=g\circ f(a_2)$ を満たす任意の元 $a_1,a_2\in A$ をとる．
合成写像の定義より $g(f(a_1))=g(f(a_2))$ ．
$g$ は単射なので $f(a_1)=f(a_2)$ であり，さらに $f$ が単射であることから $a_1=a_2$ となる．
よって $g\circ f$ も単射である．

(ii) $f,g$ を全射とする．
任意の $c\in C$ をとる．
$g$ は全射なのである $b\in B$ が存在して $c=g(b)$ ．
さらに $f$ も全射なのである $a\in A$ が存在して $b=f(a)$ と書ける．
よって $c=g(f(a))=g\circ f(a)$ となり， $g\circ f$ も全射である． $\Box$