微小正準変換

Prerequisite

無限小の正準変換を考えることは，正準形式の保存則を導く上で重要である．
保存則は作用がもっている対称性に起因するものである．
それがLagrange形式においてはLagrangianに対する（時間と座標の函数の時間の全微分項を除く）不変性を意味していた．
Lagrangianが不変ならば運動方程式が不変となる．

同様に正準形式でも作用の対称性は正準方程式の不変性に対応する．
一方で正準方程式を不変に保つ変換は正準変換であるので，両者は密接な関係にあると言える．

Noetherの定理は連続な対称性に保存則が対応するというものであった．
したがって微小変換に対して正準方程式が不変なとき，どのようなことが導けるかを調べれば良い．
微小正準変換を時間に依存しない変換として，

とおく．時間に依存する場合はゲージ変換とよばれるがここでは詳細に立ち入らない．

微小正準変換は恒等変換に近いので母函数を $\Phi(q,P)$ または $\Psi(p,Q)$ にとればよい．いまは $\Phi(q,P)$ のほうを選ぶ．
すると正準変換の母函数の性質により，

恒等変換に近いので母函数は(恒等変換) $+$ (微小変換)の形に書ける：

無限小正準変換の母函数

ただし $\epsilon$ は微小パラメータ．
これを上式に代入して整理すれば，

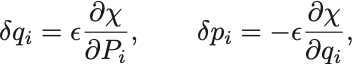
が得られる．
同じ精度（つまり $\delta$ の付いた量の1次までとる近似）で微分の $P_i$ は $p_i$ に置き換えても良い：

あるいはこの2式をシンプレクティック表現すると，位相空間上 $\Gamma$ の微小正準変換 $\boldsymbol{\xi}\mapsto\boldsymbol{\Xi}=\boldsymbol{\xi}+\delta\boldsymbol{\xi}$ に対して

ここで $\xi_i=(q_1,\cdots,q_{N},p_1,\cdots,p_{N})$ であり，

Poisson括弧のシンプレクテッィク表現と比較すれば，

微小正準変換

がわかる．
こうして，微小正準変換は母函数を用いて書くことができた．

対応するシンプレクティック行列は，

微小正準変換によるHamiltonianの変化分は

今 $\widetilde{H}=H$ なので $\delta H =0$ である．
微小変位を母函数で書けば

となり母函数 $\chi$ とのPoisson括弧が $0$ となる．
位相空間上の任意函数の時間微分はHamiltonianとのPoisson括弧に等しいことから

となり $\chi$ は保存量である．

微小正準変換の例をいくつか見ていこう．

まず微小な時間並進変換 $t\mapsto t+\epsilon$ に対しては $\epsilon$ の1次までで，

よって $\delta \xi_i=\epsilon\dot{\xi}_i$ となり，

これは $\chi$ が正準方程式を満たすことを意味している．
ゆえにHamiltonian $H$ を母函数として選べば時間並進変換が生成される．
正準方程式とは，Hamiltonianを母函数，時間を微小パラメータとする微小正準変換といえる．

Hamiltonianの時間微分は

であるが自明に $\{H,\,H\}_{\mathrm{P}}=0$ であり，Hamiltonianが保存量であるための条件は時間に陽に依存しないこと; $\partial H/\partial t = 0$ となる．

次に空間の並進変換 $q_i\mapsto q_i+\epsilon\delta_{ij}$ （ $j$ 番目の座標だけ並進変換する）に対しては，

よって $\delta q_i=\epsilon\delta_{ij},\,\delta p_i=0$ となり，

これは $\chi$ が基本Poisson括弧式を満たすことを意味している．
ゆえに運動量 $p_j$ を母函数として選べば空間並進変換が生成される．
基本Poisson括弧式とは運動量を母函数，座標を微小パラメータとする微小正準変換といえる．

運動量の時間微分は正準方程式より $\dot{p}_j=\partial H/\partial q_j$ なので，保存量であるための条件はHamiltonianが $q_j$ に陽に依存しないこととなる．

最後に3次元空間の回転変換 $q_i\mapsto \sum_jO_{ij}q_j,\,p_i\mapsto \sum_jO_{ij}p_j,\,(i=1,2,3)$ を考える（簡単のため3次元の1質点系）．
無限小回転は成分が小さい反対称テンソル $\delta\omega_{ij}$ を用いて $O_{ij}=\delta_{ij}+\delta\omega_{ij}$ とかける．
さらに $\delta\omega_{ij}$ はSO(3)の生成子 $S_k$ を用いて