正準変換の母函数

Prerequisite

時間依存しない正準変換

変数変換

を施しても正準方程式が不変なとき正準変換と定義した．
この節では運動方程式の不変性は作用またはLagrangianの不変性に込められることに着目しよう．

新旧それぞれの正準変数で定義される作用 $S[p,q]$ と $S[P,Q]$ に対して，導かれる運動方程式が不変であるためにはその違いが座標と時間の函数の全微分程度でなければならない：

作用の変分の式より軌道が運動方程式を満たし，初めの時刻の端点を固定する条件のもとでは作用を終わりの端点の時間 $t=t_1$ と座標 $q_i=q_i(t_1)$ の函数とみなすことができて

とかける． $\mathrm{d} S(Q,t) - \mathrm{d} S(q,t) = \mathrm{d} F(q,Q,t)$ より，

$\mathrm{d} F$ を計算して整理すると，

これが任意の $q_i,\,Q_i$ と $t$ で独立に成り立つためには，

$F(q,Q,t)$ が決まればこれら3式から $Q_i=Q_i(p,q,t)$ と $P_i=P_i(p,q,t)$ と新旧のHamiltonianの関係が得られる．
言い換えれば函数 $F(q,Q,t)$ は正準変換 $(p,q)\mapsto(P,Q)$ を生成する．
この $F$ を正準変換の母函数 (generating function) という．
母函数 $F$ は座標のみの函数であり，運動量がその座標微分で求められるような変換だけがこの母函数によって可能である．そのため座標変換 $Q_i=Q_i(q,t)$ のような変換を表すことができないことがわかる．

母函数の微分は，

母函数の微分 (1)

である．
この式にLegendre変換を施して $\Phi(q,P,t)$ をつくろう．つまり2つ目の関係式を $Q$ について解いて $Q=Q(q,P,t)$ を求めて，

で $\Phi(q,P,t)$ を定義する．微分は，

母函数の微分 (2)

となる．偏微分係数から，

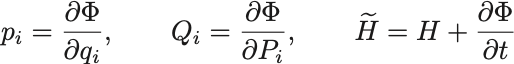
あと $F$ の $q$ をLegendre変換した $\Psi(p,Q,t)$ と $q$ と $Q$ の両方を変換した $\Xi(p,P,t)$ を考えられて，それぞれ微分は，

母函数の微分 (3), (4)

ここから導かれる関係式は，

以上から4つの正準変換の母函数 $F,\Phi,\Psi,\Xi$ が得られた．
簡単な例で母函数を具体的に求めてみよう．
まず恒等変換 $(p,q)\mapsto(P,Q)=(p,q)$ について考えよう．
$F$ で生成しようとすると $F$ の $q$ 微分と $Q=q$ 微分の $-1$ 倍がどちらも $p=P$ でなければならないが，それはどういう函数形でも不可能である．
恒等変換では $q$ と $Q$ を独立な変数として扱えないために $F(q,Q,t)$ から生成することができないのである．
では $\Phi$ ではどうかというと $\Phi=\sum_iq_iP_i$ をとれば，

となって恒等変換を生成することがわかる．
さらに $\Xi$ では生成できず $\Psi$ では $\Psi=-\sum_ip_iQ_i$ にとれば生成できる．
たしかに $\Phi$ と $\Psi$ では引数が独立に選ばれている．

次に座標変換 $q\mapsto Q=Q(q)$ の母函数を求めよう．
座標変換に伴って運動量は $p\mapsto P=P(p,q)$ と変換されるものとする．
恒等変換からヒントを得て $\Phi = \sum_if_i(q)P_i$ という形を仮定する．ただし $f$ は元の座標の任意の函数である．
このとき，

でありたしかに座標変換を生成している．運動量の変換に注目すると $\partial f_j/\partial q_i$ という因子は座標変換 $Q_i=f_i(q)$ に関するJacobi行列に等しい．座標変換が正則ならば逆変換 $q=f^{-1}(Q)$ も存在して

とかける．

母函数 $F$ の微分が積分可能であり $F$ が存在するための必要十分条件について考えてみよう．
$(p,q,t)$ を独立変数にとって $\mathrm{d} Q_i$ を元の変数 $\mathrm{d} p_i,\,\mathrm{d} q_i,\,\mathrm{d} t$ で変数変換すれば，

$\mathrm{d} F$ が $(p,q,t)$ の函数として完全微分である（ $F(p,q,t)$ が存在する）ための必要十分条件は，一般のポテンシャル論より，

である．今 $p_i,\,q_i,\,t$ は独立なことに注意してそれぞれを整理すれば

ここで新たにLagrange括弧

Lagrange括弧

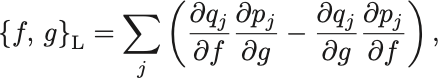
という記号を導入すると，上から3つは

と表記される（プライムは新正準変数で定義されたLagrange括弧を意味する）．
これらは基本Lagrange括弧式

基本Lagrange括弧式

が正準変換のもとで値を変えないこと示している．

基本Lagrange括弧式の不変性は基本Poisson括弧式の不変性と等価であることは簡単な連立方程式を解くことで示せる．
基本Lagrange括弧式の1つ目に $\partial Q_l/\partial q_k$ をかけて，2つ目に $\partial Q_l/\partial p_k$ をかけ，それぞれ $k$ について和をとる．その後2式の差をとれば，

一方で基本Lagrange括弧式の1つ目に $\partial Q_l/\partial p_i$ をかけて，3つ目に $\partial Q_l/\partial q_i$ をかけ，それぞれ $i$ について和をとる．その後2式の差をとれば，

得られた2式について，1つ目に $\partial q_i/\partial Q_k$ をかけて，2つ目はまず添字 $k$ を $i$ に変えてから $\partial p_i/\partial Q_k$ をかけ，それぞれ $k$ について和をとる．その後2式の和をとれば，微分の鎖法則により

が導かれる．同様の手順で $\{Q_l,\,Q_k\}_{\mathrm{P}}=\{P_l,\,P_k\}_{\mathrm{P}}=0$ が示せる．
以上により母函数が完全微分のための条件から正準変換のもとでの基本Poisson括弧式の不変性が示された．

では完全微分のための条件の残りの4つ目と5つ目の条件についても見ていこう．
4つ目に $\partial q_i/\partial P_k$ をかけ，5つ目に $\partial p_i/\partial P_k$ をかけ，それぞれ $i$ について和をとる．その後2式の和をとれば，微分の鎖法則により

同様にして4つ目に $\partial q_i/\partial Q_k$ をかけ，5つ目に $\partial p_i/\partial Q_k$ をかけ，それぞれ $i$ について和をとる．その後2式の和をとれば，

$Q_i,\,P_i$ の時間微分は $(p,q,t)$ の函数とみなすとPoisson括弧の一般的な性質により

であるが今得られた条件とPoisson括弧の不変性から新正準変数での正準方程式 $\dot{Q}_i = \{Q_i,\,\widetilde{H}\}_{\mathrm{P}}',\,\dot{P}_i = \{P_i,\,\widetilde{H}\}_{\mathrm{P}}'$ が導かれる．

以上の議論により次のことがわかる：

変換 $(p,q)\mapsto(P,Q)$ に対して

$\mathrm{d} F = \sum_ip_i\mathrm{d} q_i-\sum_iP_i\mathrm{d} Q_i+(\widetilde{H}-H)\mathrm{d} t$ が完全微分である
$\Leftrightarrow$ 基本Poisson括弧が不変かつ次の正準方程式が成り立つ:
　　 $\dot{Q}_i = \{Q_i,\,\widetilde{H}\}_{\mathrm{P}},\quad\dot{P}_i = \{P_i,\,\widetilde{H}\}_{\mathrm{P}}$

Poisson括弧の値は正準変換のもとで不変なので，変換後を意味するプライムは省略した．

Problems

$\textsc{Problem1. }$

2次元直交座標 $(x,y)$ から平面極座標 $(r,\theta)$ への座標変換の母函数を求め，極座標での運動量 $p_r,\,p_{\theta}$ を求めよ．

$\textsc{Solution. }$

座標変換 $Q_i=f_i(q)$ の母函数は $\Phi=\sum_iP_if_i$ である．
極座標への変換式は

であるから

が求める母函数である．運動量は $P_i = \sum_j\partial q_j/\partial Q_i$ なので，

となる．ベクトル表記では $p_r=\boldsymbol{p}\cdot\boldsymbol{n}$ （ $\boldsymbol{n}=\boldsymbol{r}/r$ は位置の方向ベクトル）であり，運動量の動径方向成分に等しい．他方 $p_{\theta}$ は角運動量に等しいことが見てとれる．