静電場の多重極展開

~ QuantumAtsuo

Prerequisite

電荷がある領域に局在している系を遠方から観測する

Poisson方程式の解

で，電荷がある領域に局在していてそれ以外では電荷なしの状況を考える．
この場合，無限遠で静電場が存在しない境界条件が適用できる．
このときの十分遠方での静電ポテンシャルを計算してみよう．

原点を電荷の集中する領域内にとる．
いま \rho{\boldsymbol{x}'} はこの領域でしか値を持たないから全空間積分もその有限の範囲でしか効かない．
したがって |\boldsymbol{x}|\gg|\boldsymbol{x}'| と仮定して積分できる．
以下では表記の簡単のため |\boldsymbol{x}|=R,\,|\boldsymbol{x}'|=r と書くことにする．
すると |\boldsymbol{x}-\boldsymbol{x}'|=\sqrt{R^2+r^2-2Rr\cos\theta} で \theta は \boldsymbol{x} と \boldsymbol{x}' の成す角である．
これから，

平方根の中の第2，3項は R\gg r のことから 1 より十分小さい量なのでこの量でTaylor展開できる．
展開をしていくと最初の数項は，

第1項からは，

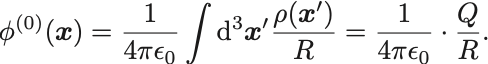
ここで Q は電荷密度の全空間積分であり系の全電荷を表す．
第1項は電荷 Q の点電荷がつくる静電ポテンシャルと等価であり，電荷の集中した領域を原点にある点電荷で近似して得られる式と同じである．

第2項からは，

ここで，

であり系の電気双極モーメントを表す．
これは領域が広がりを持っていて，その広がりと原点がつくる双極モーメントからの寄与である．
もし系の全電荷 Q が0に等しいならば双極モーメントは原点の選び方によらないことが示される．
座標変換を \boldsymbol{y}'=\boldsymbol{x}'+\boldsymbol{a} とすると，

となるが第2項の積分は全電荷であるから今は0に等しく，結局 \boldsymbol{P}'=\boldsymbol{P} であり原点の取り方によらない．
そもそも電荷が有限の領域で安定に存在するためには正の電荷と負の電荷が等量あり全電荷は0でなければならない．
したがって大抵の場合にこのことは満たされているものとしてよい．

次に第3項からは，

ここで，

は系の四重極モーメントとよばれるものである．

このようにして遠方でのポテンシャルは n 重極ポテンシャルの和で書ける．
これを多重極展開という．
多重極展開の一般項を求めてみよう．
これはすぐにわかって，上で現れたTaylor展開がLegendre多項式 P_n(\cos\theta) の母函数になっていることから，

である．
ここでLegendreの多項式は，

で表される直交多項式である（ \lfloor r\rfloor は床函数で r を超えない最大の整数を表す）．

Problems

\textsc{Problem1.}

多重極展開の一般項がLegendre多項式で書けることを示せ．

\textsc{Solution.}

表記の簡単のため t=r/R,\,\cos\theta = \alpha とおいて

の |t|<1 におけるTaylor展開をして t の n 次の係数を求める．
まずTaylor展開については

であることを用いる．
ただし n!!=n(n-2)(n-4)\cdots で1つ飛ばしの階乗を表す．
x=2\alpha t-t^2 を代入して2項展開によって

3行目へは (2n-1)!!=(2n)!/(2^nn!) であることを用いた．
いまは t の各冪の係数が知りたいので上の和を t の冪ごとの和に書き換えたい．

そのために n+k=c と固定したまま k の和をとることを考える．
図より等価な和のとり方は

である．したがって

が導かれる．よって多重極展開の式は

Next

コメントを残す