電磁波

Prerequisite

ゲージ対称性

Maxwell方程式は電荷や電流が全く存在しないところでも電場や磁場の有限な値を持つ解を許す．
そのような電磁場のみの系のMaxwell方程式を解いていこう．
電荷・電流が存在しない場合のMaxwell方程式は，

いまLorenzゲージ

に選べば，

という方程式が成立する．
この方程式を波動方程式 (wave equation) という．

波動方程式を解いていこう．
上ではLorenzゲージを採用したがさらに制限を加えて輻射ゲージに固定して，

とする．
波動方程式の時間成分は自明なので空間成分

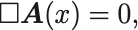
についてだけ注目する．
Fourier変換をしてみると，

となる．
これを波動方程式に代入すると，

となる．
したがって任意の $(\omega,\boldsymbol{k})$ で，

が成り立たなければならない．
これを分散関係 (dispersion relation) という．
波動方程式の解は必ず分散関係を満たさなければならず

という形をもつ．
波動方程式は線型な微分方程式なのでこれらの任意の線形結合も解である．
したがって

も解である．
第2項で $\boldsymbol{k}\mapsto-\boldsymbol{k}$ と変数変換して，四元波数ベクトル，

を導入すれば

この解はさらに制限がかかる．
まずベクトルポテンシャルは実数でなければならないので $\boldsymbol{A}=\boldsymbol{A}^*$ ．
この条件から

が任意の $\boldsymbol{k}$ について成り立っている必要がある．
次にこの方程式を解くにあたって輻射ゲージを採用していたので $\boldsymbol{\nabla}\cdot\boldsymbol{A}(x)=0$ を満たさなければならない．
解を代入すれば，

が任意の $\boldsymbol{k}$ について成り立っている必要がある．
つまり係数 $\boldsymbol{a}(\boldsymbol{k})$ は三次元波数ベクトルと直交している．
そこで $\boldsymbol{k}$ ごとに決まる2つの独立なベクトル $\boldsymbol{\epsilon}_+(\boldsymbol{k}),\,\boldsymbol{\epsilon}_-(\boldsymbol{k})$ を

となるようにとる．
ただし $\lambda=\pm$ ．
この $\boldsymbol{\epsilon}_{\lambda}(\boldsymbol{k})$ を偏極ベクトル (polarized vector) という．
そして係数を

と展開する．

以上から波動方程式の一般解は

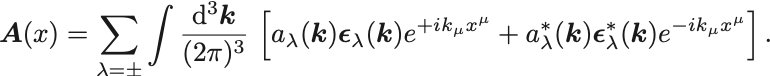
$\phi=0$ なので $\epsilon^0_{\lambda}=0$ とおいて四元偏極ベクトル ${\epsilon_{\lambda}}^{\mu}(\boldsymbol{k})$ を構成する．
すると

波動方程式の一般解

と書ける．

直交関係から三次元の任意のベクトル $\boldsymbol{V}$ は方向ベクトル $\boldsymbol{n}=\boldsymbol{k}/|\boldsymbol{k}|$ と偏極ベクトル $\boldsymbol{\epsilon}_{\lambda}(\boldsymbol{k})$ を用いて

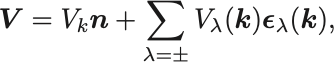
のように展開できる．
ここで $V_k=\boldsymbol{n}\cdot\boldsymbol{V}$ ， $V_{\lambda}=\boldsymbol{\epsilon}^*_{\lambda}(\boldsymbol{k})\cdot\boldsymbol{V}$ である．
これを展開式に代入すると

となる．
すなわち完全系の式，

が成立している．
これから

もわかる．
これは波数ベクトル $\boldsymbol{k}$ に直交する二次元平面への射影演算子である．
輻射ゲージをとることは任意のベクトルポテンシャル $\boldsymbol{A}$ にこの射影演算子を作用させることと等価である．

これを四次元に拡張したい．
四元方向ベクトル $n^{\mu}=k^{\mu}/|\boldsymbol{k}|=(1,\boldsymbol{n})$ を用意する．
しかし $n^{\mu}$ は分散関係によりヌルベクトル $n^{\mu}n_{\mu}=0$ であり自身と直交している．
この問題を解決するには $\boldsymbol{k}$ ごとに補助ヌルベクトル $l^{\mu}$ を用意して

となるようにとる．
今の場合 $l^{\mu}=(1/2,\,-\boldsymbol{n}/2)$ と選べば良い．
そして任意の四元ベクトル $V^{\mu}$ は

と展開できる．
ここで $V_l = -l_{\mu}V^{\mu},\,V_k= -k_{\mu}V^{\mu}$ であり $V_{\lambda}={\epsilon^*_{\lambda}}_{\mu}(\boldsymbol{k})V^{\mu}$ ．
これらより

すなわちヌルベクトルを含む場合の四次元の完全系の式，

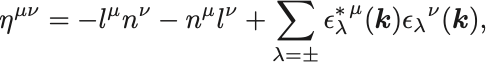
を得る．
時間方向の単位ベクトル $t^{\mu}=(1,\boldsymbol{0})$ と三次元の方向ベクトル $\boldsymbol{n}$ を四次元にしたもの $\mathsf{n}^{\mu}=(0,\boldsymbol{n})$ を導入すれば

とも書ける．
波数ベクトルに直交する二次元平面への射影演算子は

となる．

物質がないところでのMaxwell方程式の解は，波数ベクトルに直交する二次元平面内に存在する振動 $\exp(\pm ik_{\mu}x^{\mu})$ の重ね合わせである．
それゆえ四元ポテンシャルから計算される電場と磁場も振動している．
この振動する電磁場を電磁波 (electromagnetic wave) という．
真空中の電磁波の性質については節を改めて議論する．