実スカラー場の正準量子化

Prerequisite

この節では自由場（ $V(\phi)=0$ ）の正準量子化を行おう:

正準量子化の手続きはまず古典論でのPoisson括弧を計算して，それを $i$ 倍したもので交換子を定義する．

註）自然単位系なので $i\hbar=i$ であることに注意．

たとえば $N$ 粒子系では $\{p_i,\, q_j\}_{\mathrm{P}}=\delta_{ij}$ なので $[p_i,\,q_j]=i \delta_{ij}$ となる．
場についても同様の手続きをする．
Klein–Gordon場 $\phi$ の正準共役運動量 $\pi$ は，

である．
Klein–Gordon場の場合の基本Poisson括弧は $\{\phi(x),\,\pi(y)\}_{\mathrm{P}}=\delta^{(d-1)}(\boldsymbol{x}-\boldsymbol{y})$ ．
したがってKlein–Gordon場の同時刻正準交換関係は，

となる．
場の演算子は時間依存性を持つので最初からHeisennberg描像の演算子であるが，ここでは表記の簡単のためHeisenberg描像を明示する添字 $\mathrm{H}$ や同時刻であることを明示するE.T. を省いた．
上式によりKlein–Gordon場は量子化され演算子になった．
Klein–Gordon場の一般解において演算子になるのは係数 $a(\boldsymbol{k}),\,a^{\dagger}(\boldsymbol{k})$ である

場についての正準交換関係を係数についての交換関係に置き換えるために，まず一般解を $a(\boldsymbol{k})$ について解く．
運動量場を自由場展開すると，

$\phi$ に $e^{-ik'\cdot x}$ を作用させて空間積分 $\int\mathrm{d}^{d-1}\boldsymbol{x}$ したものは，

同様の計算で $\pi$ に $e^{-ik'\cdot x}$ を作用させて空間積分 $\int\mathrm{d}^{d-1}\boldsymbol{x}$ したものは

変形の際 $\omega(\boldsymbol{k})=\omega(-\boldsymbol{k})$ であることを用いた．
2つの式から $a(\boldsymbol{k})$ について解くことができて，

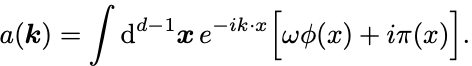
Hermite共役をとれば，

この2つの演算子 $a(\boldsymbol{k})$ と $a^{\dagger}(\boldsymbol{k})$ の交換関係は場の正準交換関係からわかって，

$[\phi(x),\,\pi(y)]=i\delta^{(3)}(\boldsymbol{x}-\boldsymbol{y})$ より空間積分の片方が実行できて，

もう一方の空間積分はデルタ函数を与えるので結局，

他の組み合わせではデルタ函数が現れたときに前後の項がキャンセルしてしまうことがわかる．
したがって，

以上が求める交換関係である．
調和振動子の量子論の議論を思い出してみよう．
調和振動子の固有値方程式を解くときにはまず正準変数 $\hat{x}_i,\hat{p}_i$ から生成・消滅演算子 $\hat{a}_i,\hat{a}_i^{\dagger}$ へ移行した．
こうすればHamiltonianが対角化され問題が容易に解けるようになる．
そのとき重要だったのが生成・消滅演算子の交換関係であった．
個数演算子 $\hat{N}=\hat{a}_i^{\dagger}\hat{a}_i$ のある固有状態 $|{n}\rangle$ に対して $\hat{a}_i$ を作用させると固有値が1つ下がった固有状態 $|{n-1}\rangle$ が得られ， $\hat{a}_i^{\dagger}$ を作用させると固有値が1つ上がった固有状態 $|{n+1}\rangle$ が得られる．
こうした結論は調和振動子に特徴的なものではなく，生成・消滅演算子の交換関係から直接導かれる性質である．
調和振動子の場合はHamiltonianが個数演算子（＋定数）でかけるので個数演算子の固有値問題をエネルギー固有値の問題にすり替えられるのである．

このような事情からKlein–Gordon場の自由場展開の係数を生成・消滅演算子と解釈することができる．
多自由度のときのラベル $i$ が今は波数 $\boldsymbol{k}$ に対応し，その変換の「Jacobian」として $(2\pi)^{d-1}2\omega$ が付されている．
Klein–Gordon場のHamiltonianは，

であり，調和振動子のHamiltonianとよく似た形をしている．

では自由場展開の式を代入して生成・消滅演算子で表そう．
煩雑な計算だがデルタ函数をうまくつかって変形していく:

ここで $a(\boldsymbol{k})$ どうしの積の項に注目してみよう．
そのような項を集めると $(-\omega\omega'-\boldsymbol{k}\cdot\boldsymbol{k}'+m^2)a(\boldsymbol{k})a(\boldsymbol{k}')$ となる．
これに平面波 $e^{i(k+k')\cdot x}$ がかかっているがこれは $\boldsymbol{x}$ 積分によりデルタ函数を与える:

これによって $\boldsymbol{k}'$ 積分ができて， $(-\omega^2+\boldsymbol{k}^2+m^2)a(\boldsymbol{k})a(-\boldsymbol{k})e^{-2i\omega t}$ とまとめられる．
しかし質量殻条件 $k^2=-m^2$ より前の係数は $0$ に等しい．
以上は $a^{\dagger}(\boldsymbol{k})$ どうしの積の項でも同様でそれらはおちる．
一方 $a(\boldsymbol{k})$ と $a^{\dagger}(\boldsymbol{k})$ の積は同じように計算すると前の係数が $(\omega^2+\boldsymbol{k}^2+m^2)$ とまとめられるがこちらは質量殻条件より $2\omega^2$ となり

となる．
さらに交換関係によって生成演算子を左にもってくると，

第2項はHamiltonianが作用する状態によらず発散している．
この項の意味を調和振動子の描像にしたがって考えてみよう．
まず $\omega/2$ という因子は零点振動に対応する．
零点振動のエネルギーは基底状態 $|{0}\rangle$ のエネルギー固有値であった．

註）自然単位系では $\hbar=1$ なのでエネルギーと振動数の次元は同じになる； $E=\hbar\omega/2=\omega/2$ ．
また波数と運動量も同じ次元になる．
自然単位系の場の理論ではエネルギー・運動量に呼称を統一して区別なく扱うことが多い．

この因子を全ての $\boldsymbol{k}$ にわたって積分しているので，いろいろな振動数の零点振動子にわたってたしあげていることになる．
そこで $\mathscr{E}=\int\mathrm{d}^{d-1}\boldsymbol{k}/(2\pi)^{d-1}\cdot\omega$ とおく．
そしてデルタ函数についてはFourier変換より $\delta^{(d-1)}(\boldsymbol{0})=\int\mathrm{d}^{d-1}\boldsymbol{x}=\mathcal{V}$ とかける．
ここで $\mathcal{V}$ は空間の全体積．
よってこの第2項全体は， $\mathscr{E}\mathcal{V}$ と書けて，空間の各点に調和振動子があり様々な振動数で零点振動しているエネルギーの総和に対応する．
$\mathscr{E}$ は零点エネルギー密度と解釈できる．
これは演算子ではなく定数であって状態によらないので，このエネルギーを真空のエネルギーと解釈することにする．
エネルギーの基準は任意なのでそれを変えてこれを $0$ にする；具体的にははじめのHamiltonianに定数項 $-\mathscr{E}\mathcal{V}$ を付け加えておく．

こうしてKlein–Gordon場の生成・消滅演算子で書かれたHamiltonianが，

となることがわかった．
この表式を生成消滅演算子に重ねて解釈するなら， $a^{\dagger}(\boldsymbol{k})a(\boldsymbol{k})$ は波数 $\boldsymbol{k}$ ，振動数 $\omega$ をもつ振動子のエネルギー準位 $n$ を返す演算子である．
こうしてふたたびHamiltonianが個数演算子の積分によって表されたので，エネルギーの固有値問題と個数演算子の固有値問題が等価になる．
次節では具体的にエネルギースペクトルを，すなわち時間に依らないSchrödinger方程式の解を調べることにしよう．