ジャイロスコープ

Prerequisite

対称コマの運動

前節で議論したように軸対称な慣性モーメントをもつ剛体コマは歳差運動や章動といった特徴的な運動を示す．
これは剛体のもつ角運動量の保存則によるものである．
ここではこの対称コマを利用したジャイロスコープを紹介する．

たとえば回転していないコマは傾いた状態で静止することはおろか直立させることすら難しく，すぐに倒れてしまうだろう．
しかし回転させて角運動量を与えることで傾いた状態を維持する歳差運動が可能になり，またコマが倒れる方向へは章動とよばれる振動運動を示す．
回転する物体が安定的に姿勢を維持できることは日常においても重要な役割を果たしている．
自転車はその一例で，自転車を漕がずに静止することは難しいが，一度漕ぎ始めれば姿勢を維持することは簡単である．
また地球が外部の複雑な重力場の中でも自転の回転軸（地軸）を一定に保つことができる．

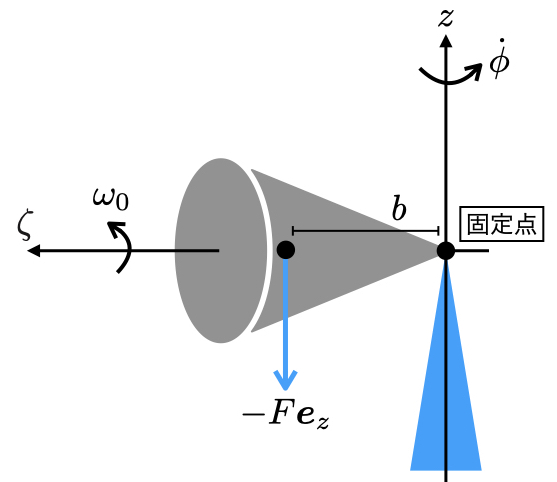
再び対称コマを考え，主慣性モーメントは $\mathrm{diag}(I,\,I,\,I')$ であるとする．
対称軸の一端を支柱の上に固定して回転運動だけを許すようにする．
そしてコマを水平（ $\theta_0=\pi/2$ ）にした状態で $\zeta$ 軸回りに角速度 $\omega_0$ を与える．
このとき剛体の角運動量は $\boldsymbol{L}=I'\omega_0\boldsymbol{e}_{\zeta}$ とかける．
慣性基準系の水平面を $xy$ 平面とし，垂直に $z$ 軸を設ける．

この対称コマに重力のような $z$ 軸の負の向きに一定の力 $\boldsymbol{F}=-F\boldsymbol{e}_z$ が重心（または $\zeta$ 軸上の任意の点）に加わると，力のモーメントは $\zeta$ に直交した方向に $\boldsymbol{N}=N_{\xi}\boldsymbol{e}_{\xi}+N_{\eta}\boldsymbol{e}_{\eta}$ として加わる．固定点から見た力の作用点の位置ベクトルを $b\boldsymbol{e}_{\zeta}$ とすれば力のモーメントは $Fb\boldsymbol{e}_z\times\boldsymbol{e}_{\zeta}$ である．
対称コマのEuler方程式より

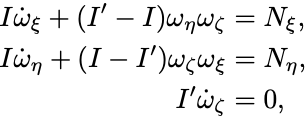
である．
ここで $N_{\xi}=\boldsymbol{N}\cdot\boldsymbol{e}_{\xi},\,N_{\eta}=\boldsymbol{N}\cdot\boldsymbol{e}_{\eta}$ である．第3式から初めに与えた角速度 $\omega_{\zeta}=\omega_0$ は保存する．
残り2つの方程式は

と変形される．

$\omega_0$ が十分速くて

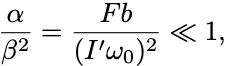
を満たす場合には前節の結果から初期条件 $\theta_0=\pi/2$ と合わせてEuler角の振動解

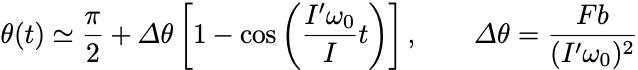
が得られる．
これは章動であるが，いまは簡単のため後ろの振動項は小さいとして無視してしまおう: $\theta(t)\sim\pi/2$ ．
したがってコマはほとんど水平を保ち続け続けながら回転する．
Euler角と角速度の間の関係式からは

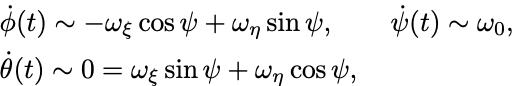
がわかる．
対称コマにはエネルギー以外の保存量として角運動量の $z$ 成分 $L_z$ があった．
その式は

であった．
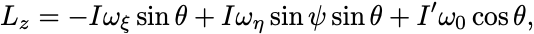
$\dot{\phi}$ の式と比較すればいまの近似のもとでは

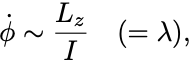
であることがわかる．
Euler角 $\phi$ は $z$ 軸周りの回転に対応していたので，対称コマは水平を保ったまま $z$ 軸周りに一定の角速度で回転することがわかった．
$\dot{\phi},\,\dot{\theta}$ の式を $\omega_{\xi},\,\omega_{\eta}$ について解けば

がわかる．
これを運動方程式に代入して整理すると

となる．
右辺については基本ベクトルの間の関係が（回転行列 $O(\psi,\pi/2,\phi)$ を用いて）

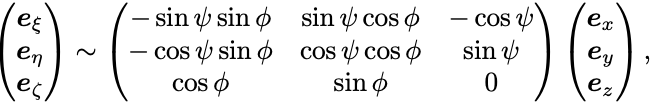
で与えられる．
これより $\boldsymbol{e}_z\sim-\cos\psi\boldsymbol{e}_{\xi}+\sin\psi\boldsymbol{e}_{\eta}$ なので $N_{\xi}\sim Fb\sin\psi$ ， $N_{\eta}\sim Fb\cos\psi$ と近似できる．
したがって

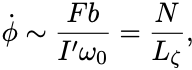
がわかる．
回転は $\omega_0$ が大きいほどゆっくりになっていく．
ここで $N=Fb\sin\theta\sim Fb$ は力のモーメントの大きさである．
これが章動を無視したときの歳差運動の本質的な部分であり単純歳差運動と呼ばれる．
簡単に言えばコマに外部から力が加えられると力の向きと直交する面内で回転する．
外部の力そのものは固定点からの抗力とつり合っているので，ここで重要な点は力のはたらく方向への（ $\theta$ まわりの）「回転」が発生しない（あっても小さく振動する）ことである．

ではなぜ $\theta$ 方向の回転が発生しないかをもう少し深く考えてみよう．
$\theta$ についての角加速度を調べていくと

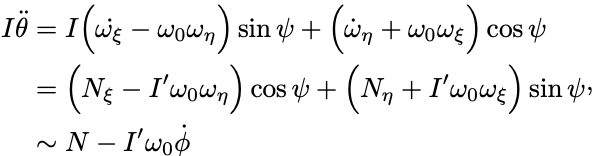
となっている．
単純歳差運動では最後の式は $0$ に等しい．
第2項が加えられた力のモーメントとつり合うので $\theta$ 方向には回転が生じないと言える．
$\dot{\phi}$ は $z$ 軸方向の角速度ベクトル $\dot{\phi}\boldsymbol{e}_z$ で，角運動量 $L_{\zeta}=I'\omega_0$ は $\zeta$ 軸方向で $L_{\zeta}\boldsymbol{e}_{\zeta}$ と書けるからこれら2つのベクトルの外積は $\phi$ による回転方向を向いている．他方で力のモーメント $\boldsymbol{N}$ は $z$ 軸の負の方向を向いたベクトル $\boldsymbol{F}=-F\boldsymbol{e}_z$ と $\zeta$ 軸方向のベクトル $b\boldsymbol{e}_{\zeta}$ との外積であった．
よって2つのベクトル $\boldsymbol{N}$ と $\dot{\phi}\boldsymbol{e}_z\times (I'\omega_0)\boldsymbol{e}_{\zeta}$ は互いに逆向きでなければならない（あるいは逆向きになるように $\dot{\phi}$ の符号，つまり歳差運動の回転方向が決まる）．

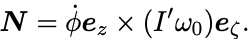
この第2項は（角速度） $\times$ （角運動量）という形をしており，もとを辿れば角運動量の時間微分のうち基本ベクトルに作用した項に由来している．
そのような項は質点の力学では遠心力やCoriolis力といった慣性力として非慣性系の運動方程式に現れた．
中でもCoriolis力は（角速度） $\times$ （運動量）という形であった．
運動方程式の対応関係 $\dot{\boldsymbol{p}}=\boldsymbol{F}\leftrightarrow \dot{\boldsymbol{L}}=\boldsymbol{N}$ と同様のことがCoriolis力についても（ $2$ 倍を除いて）成立している，と見ることができる．

自由運動の節で述べたように力のモーメントが働かない対称コマは対称軸まわりでやはり歳差運動する．
その解は

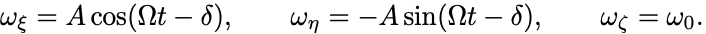
と書ける．
ここで $A,\,\omega_0$ は時間に依らない定数であり， $\Omega=(I-I')\omega_0/I$ と定義した．
初期条件をうまく選べば剛体の静止系では歳差運動しない（またはほとんど無視できる）ようにできる．
いま微小な時間 $\delta t$ だけ力のモーメント $\boldsymbol{N}$ が対称コマに働いたとすると，上述の通りにコマは $z$ 軸まわりに歳差運動を行なって回転する．
力のモーメントが作用しなくなると $\dot{\phi}=0$ なので歳差運動も止まる．
微小時間回転角の変化分は

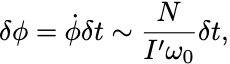
で与えられることになる．
この関係式を使えば対称コマのある時間の間の角度変化を検出することで系に働いた力のモーメントの大きさを知ることができる．

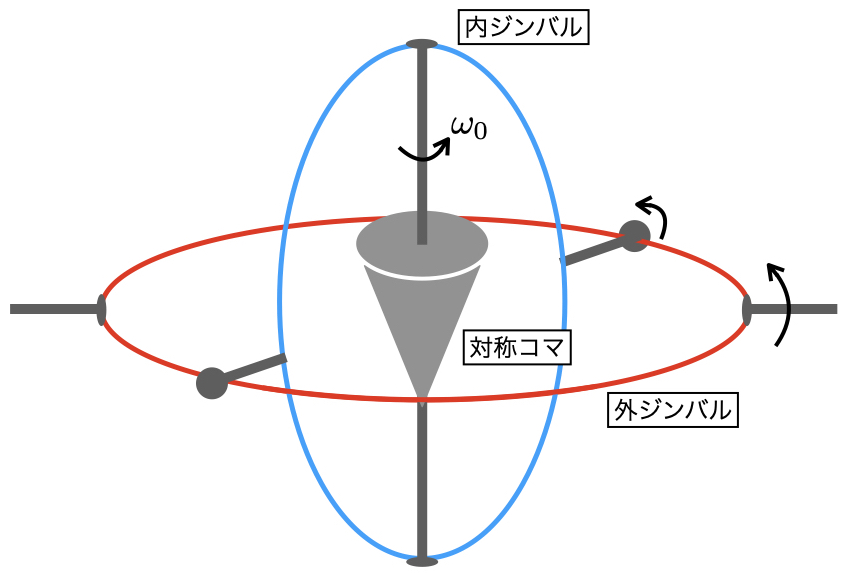
この原理を応用して物体の角速度や角加速度を検出できるようにしたものをジャイロスコープ (gyroscope) という．
ジャイロスコープには明確な固定点はないが重心のまわりに自由に回転できるようにフレームの中央に回転コマ（ローター）が固定されている．
この回転フレームをジンバル (gimbal) という．
一番外側のジンバルが航空機や船舶などに固定される．
機体が移動したり回転して角度を変えると角加速度がジンバルに生じて回転コマにはそれに応じた力のモーメントが発生する．
これから逆算して機体の回転角を計算することが可能となる．

ジャイロスコープは十分 $\omega_0$ が大きければ $\delta\phi$ を小さく抑えれるので，一定方向を維持するための器械にも応用できる．
たとえば羅針盤として設計されたジャイロコンパスがある．

剛体のNewton重力理論

“ジャイロスコープ” への1件のフィードバック

匿名より:

2023-11-14 12:35 午後

UFOの飛行手段に興味を持っている元ロボット制御系エンジニアの杉田と申します。
反重力ではないですが、重量が有り、高速で回転するコマを幾つか組み合わせて、回転方向を調整してやれば、地球（回転する天体）上で、飛行することは可能ですかね。
Coriolis力も地球が回転しているから起こる力ですよね。
また、別の考えとして、電子（電荷）が回転して磁場が発生する様に、物体（重力荷？）が回転して何かの場が発生する様な事が有ると、嬉しいのですが。
あまり物理に詳しくは無いので、奇妙なことを言っていたら、ご勘弁願います。

いいねいいね

返信