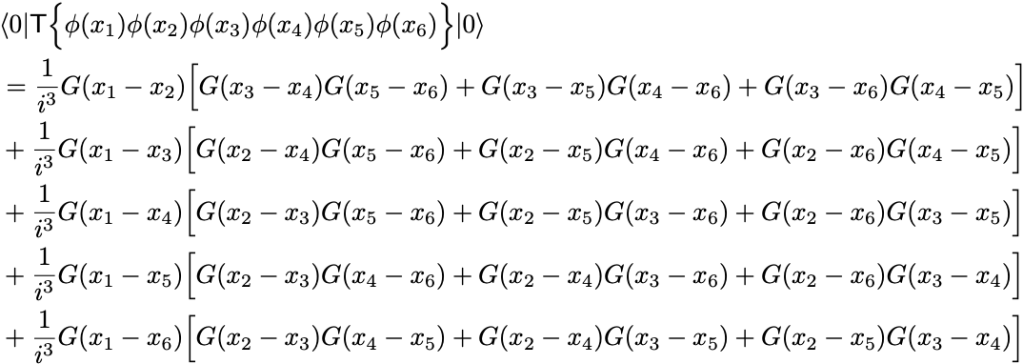Prerequisite
経路積分の計算は一般に非常に難しく,厳密に実行できるのはごく限られた場合だけである.
質点系のときは作用が積分変数についての二次形式(自由粒子や調和振動子)であればGauss積分の公式が適用できて計算が可能であった.
場の量子論において二次形式の作用は運動方程式が線型となる自由場に対応する.
自由場について経路積分が計算可能であれば相互作用がある場合の経路積分は摂動的に計算が可能となる.
そのときに便利な公式がこれから述べるWickの定理である.
自由場の理論の生成汎函数は
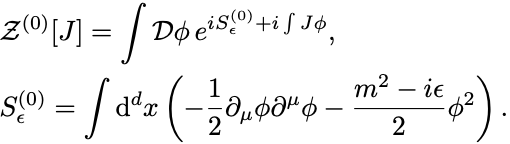
ここでも 処方を質量項に施した.
また自由場の理論であることを明示するために添字 を付けておいた.
のときの零点函数
は
に規格化しておく.

生成汎函数の指数函数の肩を二次形式にまとめよう.
作用にデルタ函数を挟み込み,運動項では部分積分を行なって微分を片方の場に寄せて
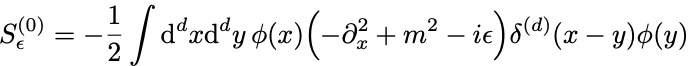
についての対称行列のような微分演算子
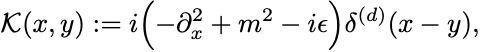
を定義する.
デルタ函数により対称性 を満たす.
を用いて指数函数は
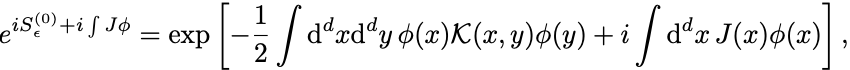
となる.
多変数のGauss積分における平方完成
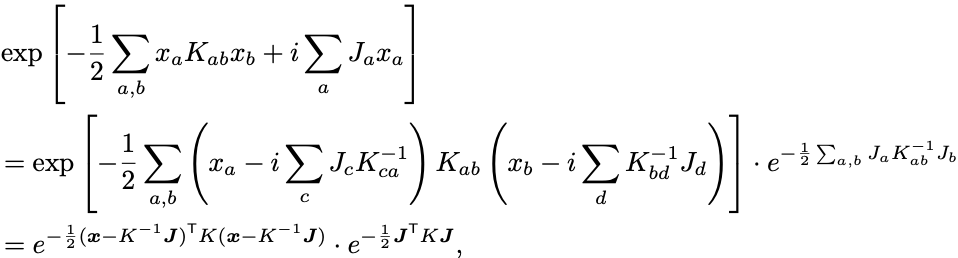
と同じように に関して平方完成をしていくと

となる.
ここで微分演算子 の逆を
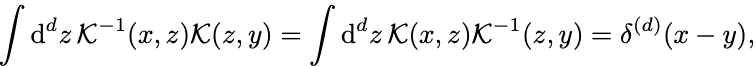
によって定義した. は引数について対称なので逆
も対称である.
あとでのこの定義の意味をもう少し詳しく調べる.
経路積分の変数変換
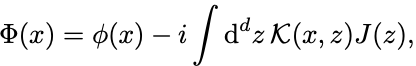
を行う.
この変数変換は汎函数積分にとっての定数シフトなので全時空の積分区間は不変である.
またJacobianは なので測度はそのまま変数だけ置き換えて
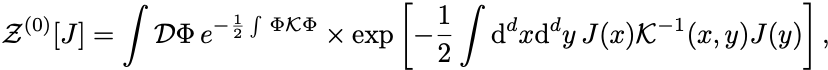
となる.
後の外場の項は積分変数によらず,経路積分の外に出せる. に関する経路積分は(時空の各点における)無限個のGauss積分なので実行できる.
しかもその値は のみに依存していて
によらない定数である.
両辺で とおくと

となる.
結局,自由場の生成汎函数について

が得られる.

では微分演算子 を具体的に求めていこう.
定義より
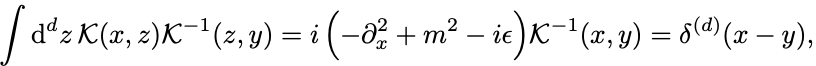
である.
これは 処方のKlein–Gorndon方程式のGreen函数
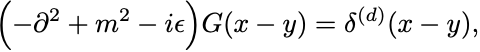
と 倍を除いて一致する.
よってGreen函数のFourier変換によるふつうの議論で は求められて
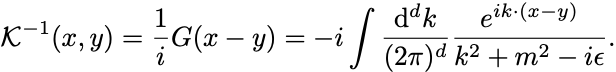
この導出過程では 処方がGreen函数の極を虚軸方向へ回避するはたらきをしている.
つまり相互作用理論でのGreen函数は必然的に2つの極 を回避する任意性(遅延函数や先進函数など)は取り除かれる.
よって生成汎函数はGreen函数 を用いて
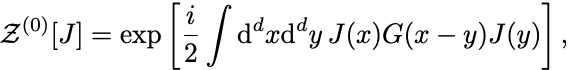
と表される.
これで準備ができたので自由場の理論における時間順序積の真空期待値の計算へ議論を移すことにしよう.
生成汎函数の性質から 個の場の真空期待値は
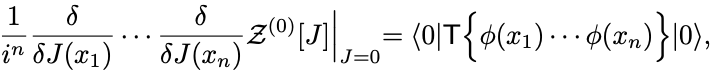
で計算できる.
他方で自由場の生成汎函数は外場の函数として表せるので,外場による微分は陽に計算可能である.
1階微分では
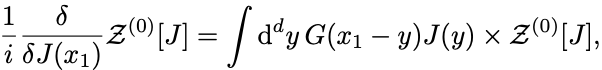
となる. とすれば右辺は
となるので

が導かれる.
自由場の真空期待値は である.
この条件は相互作用理論にも引き継がれる性質であった.
2階微分では
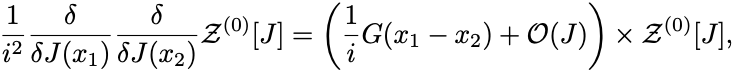
となるので とすれば
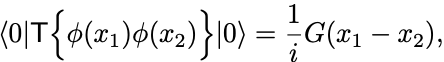
となる.
つまり自由場の二点函数はGreen函数に一致する.
任意の で求めるためにはまず生成汎函数をTaylor展開をして

とする.
明らかに の奇数次の項は存在しないので奇数個の場の積の真空期待値は
となる.
偶数次 ではGreen函数
個の積になっている.
個の外場による微分の作用の仕方は
個の
から順番に選ぶ場合の数(つまり順列)に等しく
通りの項が現れる.
外場の引数を とすると,汎函数微分によって
はこれらに置き換わる.
よって生成汎函数の 階微分の各項は

のような形をしている.
ここで は
次の置換群
の任意の元.
個のGreen函数は引数についてそれぞれ対称なので,同じものが
個ある.
さらに 個のGreen函数たちの並べ替えについても対称であり,それらは
個ある.
逆に言えばGreen函数の積を区別するのは 個の変数からのペアの作り方で,各ペアは
個だけ重複している.
これらの考察から 階微分は

すなわち 点函数は
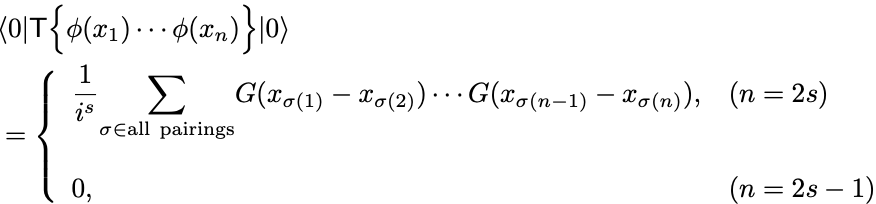
となる.
この自由場の真空期待値に関する公式をWickの定理という.
自由場の理論では,Wickの定理によって任意の個数の場の積の真空期待値を厳密に与えることができる.
例として では全てのペアは
の3通りで
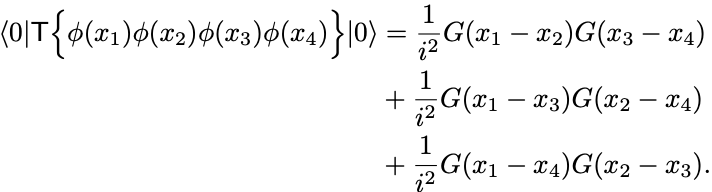
Problem
のときWickの定理のすべての項を具体的に書き下せ.
すべてのペアの作り方は 通りある: