Prerequisite
電磁場の作用は物質がないときのMaxwell方程式を与えるようなものである.
さらにすべての慣性系で物理法則は同じでなければならない,すなわちLagrangian密度はLorentzスカラーでなければならない.
そのようなLagrangian密度を探すには電場 や磁場
は三次元ベクトルであるから四次元的なものにまとめる必要がある.
そこでMaxwell方程式においてポテンシャル と
を用いて電場と磁場は,

と書けることを思い起こそう.
こうしてみると電磁場における基本的な量というのは電磁場ではなくポテンシャルの方を選んだとしても良さそうである.
基本的というのはLagrangian密度に現れる場の量として扱うという意味である.
これらのポテンシャルは

という四元ポテンシャルの形にまとめられる.
Lagrangian密度は やその1階微分
によって構成される.
次にテンソル,

を定義する.
このテンソルは定義から明らかに反対称 である.
各成分を具体的に計算してみると,


残りの成分は反対称性からわかって を行列の成分のように並べて書けば,

また上付きにしたものは,

こうして電場と磁場は一つのテンソル量にまとめられた.
この を電磁場テンソルという.
これから作られる最も簡単なスカラー量は である.
そこで電磁場のLagrangian密度を,
電磁場のLarangian密度

で定義する. は次元を合わせるために導入した真空での透磁率である.
電磁場で書きなおすには各成分をかけて和をとればよいから,

となる.
電磁場のみの系の作用は,

では に対するEuler–Lagrange方程式を見てみよう.
には依存しないから,

結局,
Maxwell方程式(1)

が得られた. のときは,

つまり電荷がないときのGaussの法則 となる.
のときは,

まとめると電流がないときのAmperè-Maxwellの法則 となる.
こうして電磁場のLagrangian密度からMaxwell方程式のうち2つが導かれた.
ただしこの2つには電荷や電流といった物質の情報が含まれていないのは当然電磁場のみので粒子を含まない系だからである.
もし荷電粒子もある系ならば電磁場との相互作用を考慮しなければならない.
そうしてMaxwell方程式に電荷や電流が入ってくるのである.
Maxwell方程式の残りの2つはなぜ現れないのかというと,そもそも電場と磁場に対してポテンシャルを導入したときにはその残りの2つの式を解いているのと同じである.
したがって四元ポテンシャルで電磁場を表現した瞬間に単磁極の非存在の式 とFaradayの法則
は仮定されているのである.
電磁場テンソルの定義というのは電場と磁場をまとめて表したものであるから,その微分について成り立つ式をあらわな形で表現しておこう.
電磁場テンソルを微分すると のような項が現れる.
微分は可換なのでこの量は と
の入れ替えについて対称である.
したがって四次元のLevi-Civita記号 と縮約すれば

が成立する. と
について反対称化して,
Maxwell方程式(2)

これは について4成分の方程式である.
のときは

であり なので
となる.
のときは
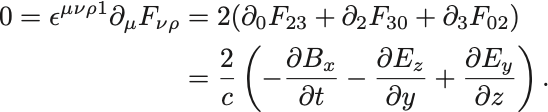
も同様で
となる.
以上で荷電粒子がない電磁場だけのLagrangian密度からMaxwell方程式が導出されることを見た.
はあらわな座標依存性がないからエネルギー運動量テンソルは連続の式を満たす.
Noetherの定理から

ここで である.
作用がLorentz対称性を持つ場合,エネルギー運動量テンソルが対称でければならないことを思い起こそう.
今得られた表式では第1項が対称でない.
そこで の両辺に
を足そう.
この左辺は対称なものと反対称なものの縮約になっているので恒等的に0である.
左辺の添え字が の微分をばらすとMaxwell方程式から電磁場テンソルの発散は
に等しいので
のみとなる.
するとエネルギー運動量テンソルの第1項と合わせて電磁場テンソルの積 が作れて,
電磁場のエネルギー運動量テンソル

となる.
これは明らかに と
について対称な形である.
トレースをとると,

となり,電磁場のエネルギー運動量テンソルはトレースレスであることがわかる.
電磁場のエネルギー運動量テンソルの成分を調べていこう.
まず 成分は,

である.
これは電磁場のエネルギー密度に一致する.
成分は,

となる.
ここで はPoyntingベクトルでエネルギーの流密度である.
4つあるNoetherカレントのうち についての連続の式は,

これは電磁場のみの系におけるエネルギー密度の保存則である.
最後に 成分を計算すると,

となりこれはMaxwellの応力テンソルである.
残っている3つのNoetherカレントに対する連続の式は運動量密度の保存則となる:

次の節では荷電粒子と電磁場が共存する系での解析力学を構築していこう.
