グランドカノニカル分布

Prerequisite

カノニカル分布

この節では熱浴と粒子浴に接した系の確率密度函数を定める．
このような系はグランドポテンシャル

が重要な役割を果たすと予想できる．

熱力学での粒子浴とは着目系と粒子のやりとりをして化学ポテンシャル $\mu$ で一定となるように制御できる系であった．
熱浴は着目する系よりさらに膨大な自由度をもつ系として定義するので，粒子浴は粒子数が非常に大きい系として定義できる．
エネルギーも遥かに大きく，全エネルギーを $E^{(\mathrm{tot})} = E + E^{(\mathrm{env})}$ としたとき， $E\ll E^{(\mathrm{env})}$ である．

系全体としては孤立系なのでミクロカノニカル分布の議論が適用できる．
つまり等重率の原理を仮定して，確率密度函数は定数

とする．
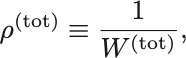
$W^{(\mathrm{tot})}$ は系全体の状態数である．
この状態数を着目系と熱浴の部分に分離することを考える．
状態数は定義より

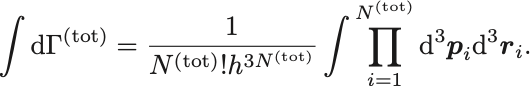
添字 $(\mathrm{tot})$ は全系に関する物理量であることを表す．
測度については注意が必要となる．
着目系の粒子数 $N$ は確率的には $0$ から $N^{(\mathrm{tot})}$ までを取りうるので，測度の分離も定数因子を $C_N$ として

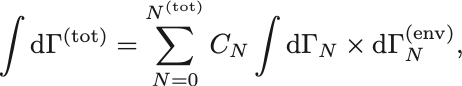
と足し上げる必要がある．
下付きの添字 $N$ は着目系の粒子数が $N$ の場合であることを明示している．
今は粒子数の依存性が重要なので $C_N$ を評価しておこう．
Planck定数は $C_N$ には寄与しない．
階乗について左辺の全系の測度には $1/N^{(\mathrm{tot})}!$ が現れ，右辺には $1/N!$ と $1/N^{(\mathrm{env})}!$ が現れている．
よってこの差異

が $C_N$ には寄与する．
一方 $N^{(\mathrm{tot})}$ から $N$ を選んで分離するには ${}_{N^{(\mathrm{tot})} }\mathrm{C}_N$ の重複が存在することに注意する．
この重複と階乗の因子がちょうどキャンセルして $C_N=1$ が結論される．

この積分のもとでHamiltonianは $H^{(\mathrm{tot})} = H_N + H_N^{(\mathrm{env})}$ と分離できる．
ここへ着目系のエネルギーに関するデルタ函数 $\int\mathrm{d} E_N\delta(H_N-E_N)=1$ を挟み込んで

とする．
カノニカル分布のときと同様の変形によって

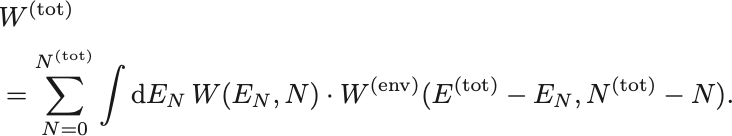
ここで

はそれぞれ粒子数が $N,\,N_N^{(\mathrm{env})}$ ，エネルギーが $E_N,\,E_N^{(\mathrm{env})}$ のときの着目系と熱浴の状態数である．

熱浴の状態数 $W_N^{(\mathrm{env})}( E^{(\mathrm{tot})}-E_N ,\, N^{(\mathrm{tot})}-N)$ に近似を施す．
熱浴にとって着目系は小さいのでほとんど孤立系とみなせるとすると，Boltzmannの式が適用できて

が成り立つ．
状態数の対数をとったものをTaylor展開で評価すると

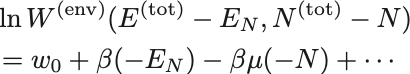
第1項の $w_0=\ln W^{(\mathrm{env})}(E^{(\mathrm{tot})},\,N^{(\mathrm{tot})})$ は定数項．
第2項の

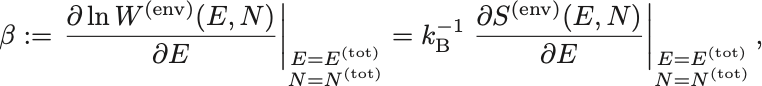
は熱浴の逆温度．
第3項の

は熱浴の化学ポテンシャル．

第4項以降については体積あたりのエネルギー $e=E/V$ とエントロピー $s=S/V$ ，密度 $n=N/V$ を導入すると

なので熱浴の体積 $V^{(\mathrm{env})}$ の冪で抑えられる．
よって熱浴の体積が着目系に比べて遥かに大きいならば

が成立する．
よって全状態数の式は

と表すことができる．
ここで $C=e^{w_0}$ ．
$W(E_N,N)$ のデルタ函数によってエネルギーの積分を実行してしまえば，Hamiltonianに置き換わって，

が得られる．
$\Xi=W^{(\mathrm{tot})}/C$ は $N$ にも依存しない定数因子．
これは確率密度函数

グランドカノニカル分布

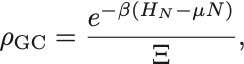
の規格化条件である．
確率度函数 $\rho_{\mathrm{GC}}$ は着目する系の確率分布を与えており，着目系のグランドカノニカル分布 (grand canonical distribution) と呼ばれる．

定数因子は規格化条件から

大分配函数

と求めることができる．
$\Xi$ は大分配函数 (grand partition function) といい，カノニカル分布における分配函数に対応する量である．
$N^{(\mathrm{tot})}$ は非常に大きいので実際の計算では $N^{(\mathrm{tot})}\to\infty$ としてしまうことが多い．

物理量 $A$ の期待値は

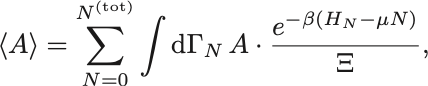
で計算される．
系のエントロピーは一般に $S=-k_{\mathrm{B}}\langle \ln\rho\rangle$ であったから，グランドカノニカル分布を代入すると

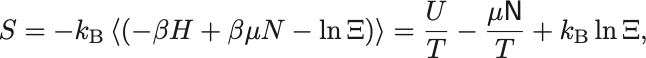
ここで内部エネルギー $U=\langle H\rangle$ ，粒子数 $\mathsf{N}=\langle N\rangle$ ，温度 $T=(k_{\mathrm{B}}\beta)^{-1}$ ．
グランドカノニカル分布から計算される期待値は温度と体積，化学ポテンシャルの函数になっている．
よって $-k_{\mathrm{B}}T\ln \Xi = U - TS - \mu\mathsf{N}$ と変形すれば，