Prerequisite
この節では角運動量を量子化しよう.
Newton力学の章で見たように角運動量は中心力場があるときに重要な役割を果たしていた.
原子や分子に働く最も典型的な力も中心力場であるので角運動量の量子論は重要である.
またスピンやアイソスピンといった素粒子の内部自由度も角運動量と同じ性質をもつオブザーバブルで記述できる.
まず角運動量の古典的な定義を思い起こすと,
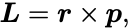
であった.
そこで正準量子化の手続きをおこなって角運動量演算子を,

によって定義する.
座標と運動量の正準交換関係から角運動量の成分どうしの交換関係がわかる.
外積をLevi-Civita記号で と書いて,
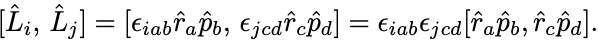
以降ではEinsteinの縮約規則を採用して1つの項に同じ添字が現れたときは和をとっているものと約束する.
Leibniz則から,
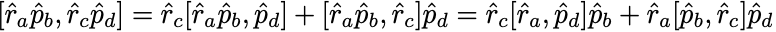
正準交換関係 より,
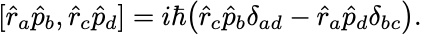
ゆえに,
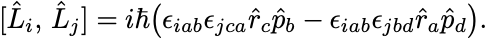
公式 より,
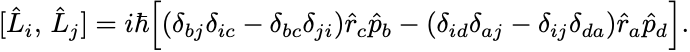
あとは単純な計算を行えば,
角運動量の交換関係
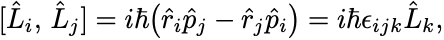
が導かれる.
この交換関係はPoisson括弧式と交換子の対応規則を仮定しても得られる:
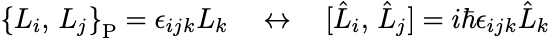
式を簡略化するために角運動量演算子を で定義し直す.
すると交換関係は となる.
角運動量の成分は一般に交換しないのでこれらの同時固有状態は構成できない.
しかしながら角運度量の大きさの演算子 との交換関係をみてみると,
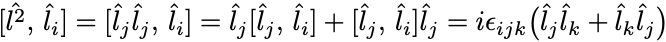
右辺は反対称と対称なものの縮約なので である.
つまり角運動量の大きさと各成分は可換であり同時固有状態が構成できる.
ただし成分同士は可換でないのでたとえば大きさと 成分の同時固有状態は構成できるが
成分は同時に固有状態になれない.
と
の同時固有状態を
とおいて

が成り立っているとしよう.
さらにこれら固有状態は正規直交化されているとしよう:
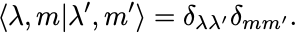
各 は物理量だから自己共役演算子でなければならないという要請から,
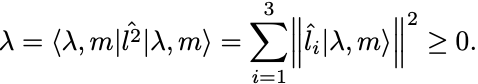
よって がわかる.
もともと角運動量の大きさの固有値であるからこれは当然満たされなければならない不等式である.
では次に,
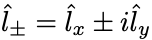
という演算子を定義する.
それぞれ上昇・下降演算子 (ladder operator) という( が上昇演算子,
が下降演算子).
上昇・下降演算子によって作られる新たな状態ベクトル について考えてみよう.
角運動量の大きさの演算子を作用すると,
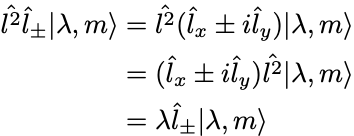
より が属する
の固有値は同じく
.
しかし角運動量演算子の 成分の固有値は,
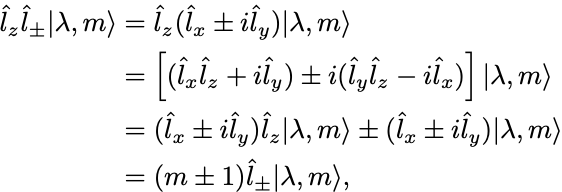
となって上昇演算子に対しては固有値が1増え,下降演算子に対しては固有値は1減る.
上昇演算子を次々に作用させていけばより大きな固有値に属する状態を作れる.
下降演算子についても同様である.
ただしその固有値には上限と下限が存在することが示せる. より,
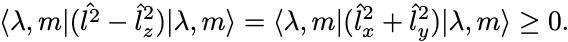
一方固有ベクトルであることから,
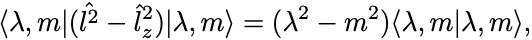
2式よりノルムは非負だから となって,
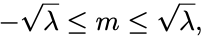
だから上限と下限を持つ. の最大値を
とすると属する状態ベクトル
にこれ以上上昇演算子を作用させてもその状態は固有値を持つことができない.
したがって次のことが成り立たなければならない:
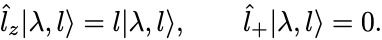
このとき,
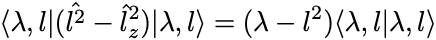
であり一方で非可換性に注意して,
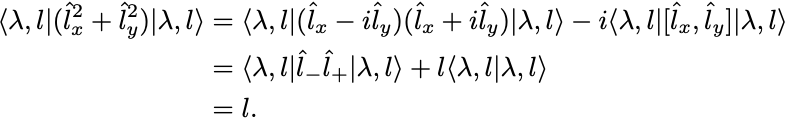
したがって ,すなわち最大の固有値
は
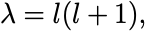
を満たす.
同様にして の最小の固有値を
とすると,
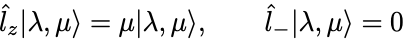
が成り立たなければならない.
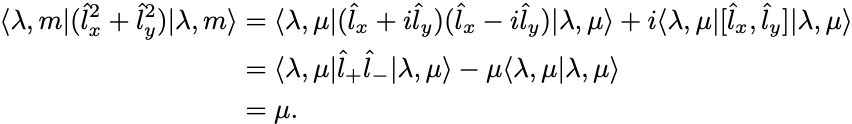
したがって .前の結果と合わせれば,

これより の固有値の最小値は
となるが,
の場合
の最大性に反するので不適.
よって の最小値は
と定まる.
以上から の固有値は与えられた
に対して,

の全部で 個の値を取りうる.
同時固有状態はラベル の代わりに
を用いて
と表記して
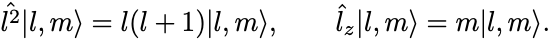
各状態 は
成分が
通りの異なった状態をとることができる.
上昇・下降演算子の性質からかつ
でなければならない.よって
は
,正の整数,あるいは正の半整数:
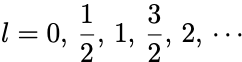
に限られる.
角運動量演算子は離散的な固有値をもつ.
この節の最後に上昇下降演算子によって固有値が1だけ異なる状態の規格化定数を定めておこう.
そこで,

とおく. であったから,
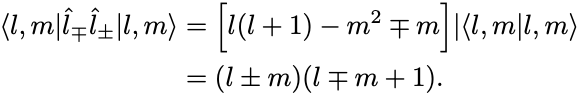
また,
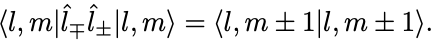
いま状態ベクトルは規格化されているとすると,
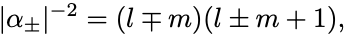
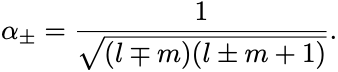
ただしCondon–Shortleyの規則にしたがい に選んだ.
ゆえに
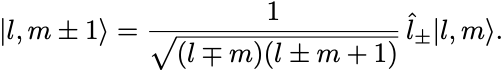
この節の議論で注目すべきことはいま得られた結果の全ては,角運動量の交換関係さえ仮定すれば古典的な定義を用いずに導出されるということである.
いいかえれば同じ交換関係を満たす全ての演算子は同じ関係式を満たすのである.
次の節では同時固有状態 などの座標表示を求める.
