時間に依る摂動論

Prerequisite

系のHamiltonianが

のように既知の項 $\hat{H}_0$ と微小パラメータ $\lambda$ がかかった時間依存する摂動項 $\hat{V}(t)$ でかけるとする．
$\hat{H}_0$ に関しては定常な固有値と固有ベクトル

がわかっている．
ここで $0$ は摂動を受けていない量であることを明示している．
簡単のため縮退はないと仮定しておこう．

初期状態を固有ベクトル $|{n;0}\rangle$ としてその任意の時刻における時間発展は相互作用描像で

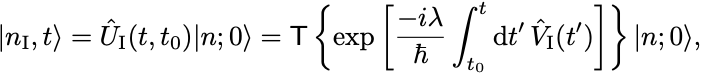
と書ける．
ただし $\hat{V}_{\mathrm{I}}(t)$ は相互作用描像における摂動項で

と定義される．
$|{n_{\mathrm{I}\rangle},t}$ を摂動なしの固有状態で展開して

とするときの係数 $a_{mn}(t)$ は

によって定義される．
言い換えるとこの係数は相互作用描像の時間発展演算子 $\hat{U}_{\mathrm{I}}(t,t_0)$ の行列要素である．
$\lambda$ は小さいのでその冪展開の最初の2項を見てみよう．

とおくと正規直交関係から $a_{mn}^{(0)}=\delta_{mn}$ であり，

である．
摂動項をSchrödinger描像に戻せば

となる．
こうして一次近似でのエネルギー固有状態の摂動による時間発展が

と求まった．
第1項と第2項のうち $m=n$ の項は元のエネルギー固有状態である．
第2項のうち $m\neq n$ の項は初期状態 $|{n;0}\rangle$ が別のエネルギー固有状態へ遷移する確率の重みを表しているので $a_{mn}^{(1)}$ は状態 $|{n;0}\rangle$ から $|{m;0}\rangle$ への遷移振幅 (transition amplitude) と呼ばれる．
つまり $m=n$ と $m\neq n$ に分けて

と書ける．

摂動が有限時間だけはたらく場合を考える．
このとき初期状態を十分過去 $t_0\to-\infty$ で用意すれば摂動のないときの定常状態 $|{n;0}\rangle$ に選べる．
また十分未来 $t\to\infty$ でも摂動の影響がないので一般に定常状態 $|{n;0}\rangle$ の重ね合わせの状態にあると仮定できる．
時刻 $t$ における任意の状態 $|{\psi,t}\rangle$ においてエネルギー固有値が $E_m$ （ $n\neq m$ ）である確率はBornの確率規則から $\mathsf{P}_m(t)=|\langle{m;0|\psi,t}\rangle|^2$ で計算される． Schrödinger描像から相互作用描像 $|{\psi_{\mathrm{I}},t\rangle}$ へ移せばこの確率は

と書き換えられる．
一次までの式を適用して位相因子が落ちることに注意すれば

となるので確率 $\mathsf{P}_m(t)$ は状態 $|{n;0}\rangle$ から $|{m;0}\rangle$ への遷移確率と呼ばれる．

摂動が周期的な場合

を考えよう．
$\hat{F}$ は時間に依存しない演算子であり， $\hat{V}$ は自己共役 $\hat{V}^{\dagger}=\hat{V}$ である．
$\hat{V}$ の行列要素は

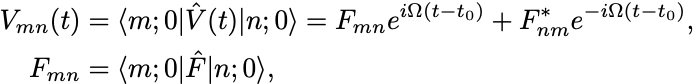
である．
一次の遷移振幅は

ここで表記の簡単のために

とおいた．
時間 $t'$ の積分は容易に実行できて

摂動計算においては $\lambda a_{mn}^{(1)}(t)$ は $1$ に比べて小さくなければならない．
したがって摂動論が有効であるためには分母 $\varDelta\omega_{mn}\pm\Omega$ が $0$ に近い値になってはいけない．
すなわち少なくとも任意の $m$ に対して