摂動の断熱定理

Prerequisite

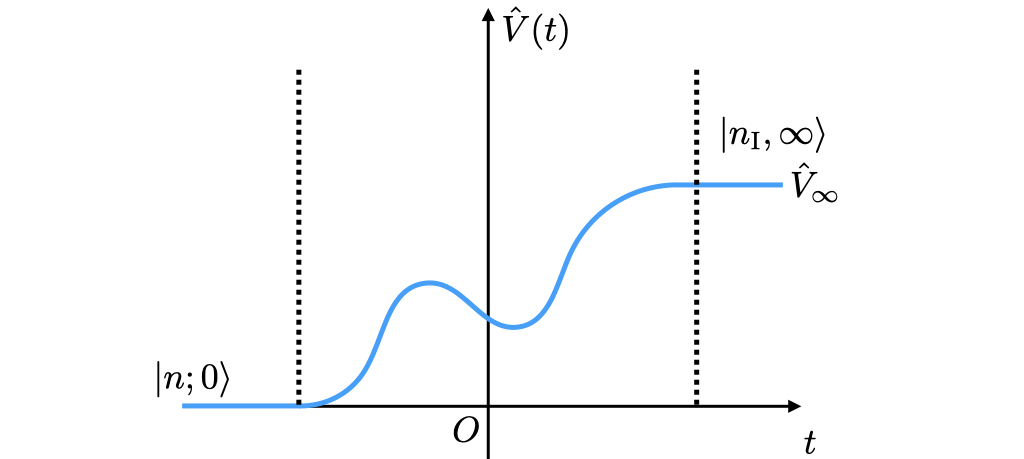
この節では摂動の形として

を満たすものを考える．
つまり十分過去では系は既知のHamiltonian $\hat{H}_0$ の固有状態で記述でき，十分未来では時間依存しない摂動 $\hat{H}_0+\lambda\hat{V}_{\infty}$ の固有状態で記述できる．

初期状態として $\hat{H}_0$ の $n$ 番目の固有状態 $|{n;0}\rangle$ を用意する．十分未来では別の定常状態の組み $|{n',\infty}\rangle$ が存在すると仮定する．初期状態は時間発展して摂動の影響を受けた後に色々な $|{n',\infty}\rangle$ の重ね合わせに遷移すると考える．相互作用描像における任意の時刻 $t$ での状態ベクトル $|{n_{\mathrm{I}},t}\rangle$ を摂動なしの固有状態で展開して

このとき遷移振幅 $a_{mn}(t)$ は摂動パラメータ $\lambda$ の冪級数として

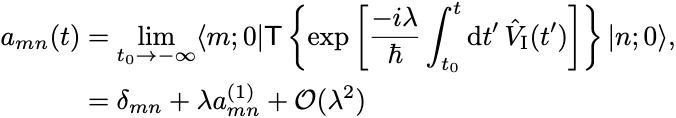
と展開される．
ここで一次の遷移振幅は

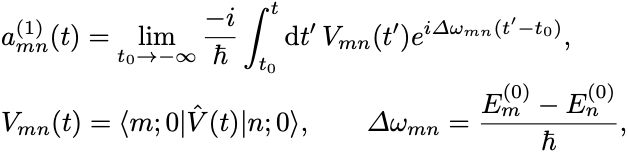
である．
さらに十分未来の極限 $t\to\infty$ をとった遷移振幅を評価したい．
いま摂動ポテンシャルに関しては境界条件が与えられているので部分積分を実行して境界項を作ってみる．
すると任意の $m\neq n$ に対して

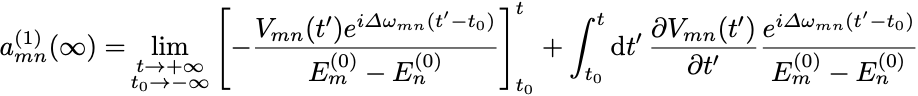
第1項の境界項については $t_0\to-\infty$ でポテンシャルは消えるからこの寄与はない．
一方で $t\to\infty$ の方は

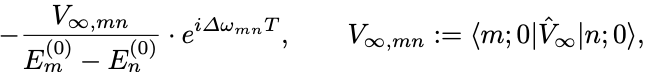
の寄与を与える．
ここで $T:=t-t_0\to\infty$ は無限大の定数である．
この項は位相因子を除いて時間依存しない摂動 $\hat{V}_{\infty}$ の一次の係数に一致していることに気づく．

そのことを見るために十分未来の固有状態の摂動論を調べておこう．
固有状態を $|{n',\infty}\rangle$ として

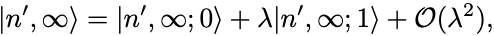
と摂動展開する．
$0$ 次の項は十分過去と同じ固有状態に選べる; $|{n',\infty;0}\rangle=|{n';0}\rangle$ ．
（縮退のない）時間に依らない摂動の一般論から

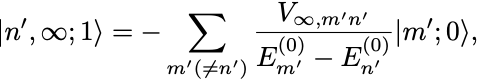
と定められる．
したがって一次までの近似で $t\to\infty$ における状態ベクトルは

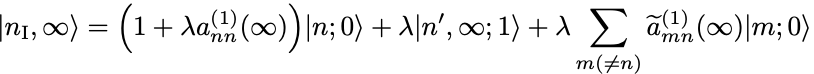
ここで

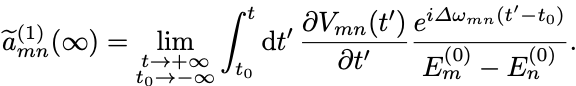
さらに右辺の第1項と第2項は一次近似の範囲で $|{n,\infty}\rangle$ の定数倍とみなすことができる．
以上より

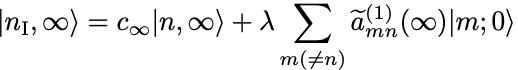
を得る（ $c_{\infty}$ は複素定数）．

初期状態 $|{n;0}\rangle$ から十分未来の固有状態 $|{l,\infty}\rangle$ への遷移振幅は，同じ精度で $\langle{l,\infty|m;0}\rangle\simeq\langle{l,\infty|m,\infty}\rangle=\delta_{lm}$ であることに注意して

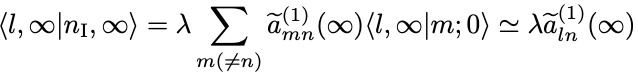
となる．
これらは $|{n_{\mathrm{I}},\infty}\rangle$ を完全系 $|{l,\infty}\rangle$ で展開したときの一次の係数である．
遷移確率は

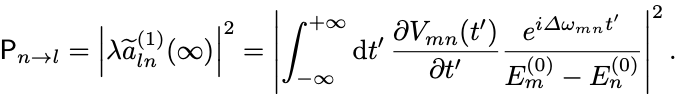
遷移確率は摂動ポテンシャル（の行列要素）の時間微分 $\partial V_{mn}/\partial t$ に依存している．
もしポテンシャルが非常にゆっくりとしか変化しない場合，遷移確率は小さくなる．
エネルギー差 $E_m^{(0)}-E_n^{(0)}$ から作られる時間スケール $\tau_{mn}=\varDelta\omega_{mn}^{-1}=\hbar/(E_m^{(0)}-E_n^{(0)})$ の間で摂動 $\hat{V}$ の時間変化を無視できる場合， $\textsf{P}_{n\to l}\simeq 0$ と近似できる．
つまり初期状態 $|{n;0}\rangle$ から $|{l,\infty}\rangle\,(l\neq n)$ への遷移は起こらず単に $|{n,\infty}\rangle$ に遷移する．
非常にゆっくりと摂動を変化させたときは前後の固有状態 $|{n;0}\rangle$ と $|{n,\infty}\rangle$ を考えれば十分といえる．
この事実を断熱定理 (adiabatic theorem) という．
摂動論を超えて，系のHamiltonianがゆっくりと変化する場合の断熱定理については後の節で幾何学的により詳しく議論することにする．