断熱不変量

Prerequisite

位相空間

系のHamiltonianには基本変数以外に質量などのパラメータが現れる．
これらパラメータは系を特徴付けている．
たとえば調和振動子は角振動数 $\omega$ （バネのときはバネ定数 $k$ ）を持ち，Coulomb力はそのポテンシャルの係数 $\alpha$ （Newton重力のときはNewton定数 $G$ と質量）を持つ．

Hamiltonianの持つパラメータが外的な要因によって時間変化することを考えよう．
あるいは時間依存するような（何らかのパラメータで特徴付けられる）外力の項が含まれる場合を考える．
もし外的要因が質点の運動を短い時間の間に大きく変えてしまうならば，その影響は無視できず運動方程式に適切に取り入れなければならない．
しかしもしゆっくりとしか運動を変えないとき，Hamilton形式において一般的な性質を導くことができる．

まず「外力の影響がゆっくり」ということを定量的に表現したい．
質点の軌道が有界な領域にとどまっているとする．
これは軌道が周期的であると言い換えられる．
この周期の典型的な大きさを $T$ とする（周期は常に一定でなくてもよい）．
そして周期運動の軌道の外力による変化がわかるような時間スケールを $\tau_{\mathrm{ex}}$ とする．
すると「外力の影響が小さい」とは $T\ll \tau_{\mathrm{ex}}$ と定式化できるだろう．
外力を特徴付けるパラメータを $\lambda(t)$ とおくと， $\tau_{\mathrm{ex}}$ は $\lambda$ の時間変化率の逆数（i.e. $\lambda$ の変化が顕著になる時間スケール）とおおよそ等しい．
したがって，

のとき外的要因の変化は質点の軌道にとってゆっくりである．

外的要因によりパラメータがゆっくりと変化する1次元1質点系のHamiltonianを $H(p,q;\lambda)$ と書こう．
パラメータがあらわに時間依存するので系のエネルギー（定義よりHamiltonianに等しい）は保存しない： $E=E(t)$ ．
実際エネルギーの時間変化は，

とかける．

いま，われわれが興味があるのは質点の運動そのものではなくて，外的要因によるゆっくりな変動の性質である．
ゆえに質点の運動の周期にわたって各物理量を時間平均してしまうことでそれを無視し，ゆっくりな時間変化だけに注目することにする．
1周期にわたっての時間平均操作は，

と定義される（数列の算術平均を函数に拡張したものとして理解できる．詳しくは統計力学の章で扱う）．
エネルギー変化を1周期にわたって時間平均すると，

となる．
ただし $\lambda$ の時間変化はゆっくりなので，1周期の間は定数とみなすことができて積分の外に出した．
ここまで周期 $T$ の定義が曖昧なので，これを式で定義しておく必要がある．
1周期の間に $\lambda$ は定数と思っているので，外的要因が時間変化しないときの質点の軌道の周期を $T$ とする，

Hamilton方程式より，

となる．
エネルギー変化の式の積分で変数変換 $q=q(t)$ を行うと，

より，

この式の右辺は $\mathrm{const.}\times\dot{\lambda}$ という形になっていることに注意しよう．
つまり外的要因の時間変化に対するエネルギーの変化はそれと同程度のゆっくりとした変化である．

次なる興味はゆっくり変化する $\lambda$ とエネルギー $\overline{E}$ を用いて，ゆっくりな変化の間の不変量を構成できないかという問題である．
そこで上式の積分に現れる量を計算しよう．
偏微分がどの変数を止めて実行しているのかを明示して書くと，

$p,\,q,\,\lambda$ は独立変数なのでJacobianを導入して計算すると，

また積分の中では $\lambda$ が定数であり，ゆえにエネルギーも保存している．
方程式 $E=H(p,q;\lambda)$ に関して，Jacobianの関係式，

が成り立つ．
したがって，

分母を払って整理すると，

となる．この事実から

断熱不変量

という量を定義すると，その周期平均の時間微分について，

が成り立つ．
$I$ という物理量は外的要因のゆっくりな変化の間に不変に保たれる量であり，断熱不変量 (adiabatic invariance) と呼ばれる．

断熱不変量をエネルギーで微分すると，

$q=q(t)$ の変数変換により

となり角振動数の逆数に等しいことがわかる．

断熱不変量の積分の中の $p$ は軌道 $q=q(t)$ に沿って $q$ を動かすときエネルギー一定の超曲面 $E=H(p,q;\lambda)$ 上を動く．
したがって断熱不変量の定義は，

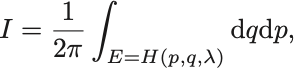
とも書くことができる．
これはすなわち位相空間内のエネルギー一定の閉超曲面 $E=H(p,q;\lambda)$ が囲む「体積」を計算していることに（ $(2\pi)^{-1}$ の因子を除いて）等しい．

調和振動子の例で断熱不変量を計算してみよう．
この系のHamiltonianは

で，今パラメータ $\omega$ が時間とともにゆっくり変化するとする．
系のエネルギー $E=H(p,q;\omega)$ を運動量 $p$ について解くと

これを断熱不変量の式へ代入して，

変数変換 $m\omega q=\sqrt{2mE} \sin\theta$ を行ない，周回積分なので $\theta$ は $0$ から $2\pi$ の値を動ことに注意して計算を進めると，

がわかる．
エネルギー保存の式は $1=p^2/(2mE)+q^2/(2m^{-1}\omega^{-2})$ と書くと，これは長径・短径が $\sqrt{2mE},\,\sqrt{2/(m\omega^2)}$ の楕円を表していて，その面積は $\pi \sqrt{2mE}\times\sqrt{2/(m\omega^2)}=2\pi E/\omega=2\pi I$ に等しい．