Lorentz変換の表現論

Prerequisite

前節では時空の並進変換とLorentz変換の生成子が対応するNoetherチャージであることを見た．
これらのNoetherチャージはチャージは正準量子化により閉じた交換関係を満たす．
さて時空の並進変換に対する理論の対称性はエネルギー運動量テンソルの保存則を導く．
Lorentz対称性からはこのテンソルが対称であることを要求するが，Lorentz変換は場の理論に対するさらなる制約を導ける．
並進変換に対してベクトル場は不変であるが，Lorentz変換に対してはベクトルと同じようにその成分が変換される．
実スカラー場以外の場の理論を議論する場合，どのようなLorentz変換性をもった場が許されるのかをこの節では見ていくことにする．

古典系におけるPoisson括弧でかける生成子から量子論へ移行する正準量子化の手続きをLorentz変換にも適用しよう．
すなわちLorentz変換の生成子が満たすPoisson括弧式，

を正準量子化しLorentz対称性をもつ任意の場の量子論に対し交換関係，

を仮定しよう（Lorentz代数）．
あるいは前節でLorentz変換の準同型性を仮定して導いた交換関係

において $S_i=\frac12\epsilon_{ijk}M^{ij},\,K_i=M^{i0}$ とおくことで同じ交換関係を導くことができる．

ここで新たな演算子として

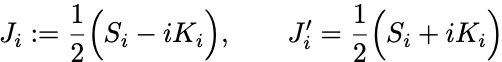
を導入する．
これらの演算子は以下の交換関係を満たしている:

これはLorentz代数が2つの $\mathrm{SU}(2)$ のLie代数に分解されることを示している．
量子論の言葉で言えば $J_i$ と $J_i'$ は可換なので同時固有状態が存在する．
そしてそれぞれ角運動量と同じ交換関係を満たすことから $J_z,\,J^2$ と $J_z',\,(J')^2$ の同時固有状態として

とできる．
各固有値は

をとることができる．

角運動量代数の性質から組み $(j,j')$ で指定される既約表現に分解される．
既約表現の次元は $d_{j,j'}=(2j+1)(2j'+1)$ である．
既約表現の中で任意の状態はラベル $m,m'$ とそれ以外の物理量や内部自由度に対応したラベル $\lambda$ で指定できる．
同じ $\lambda$ をもった状態は $d_{j,j'}$ 個の基底で展開できるベクトルと同一視できる．
いまは簡単のためにこのようなラベル $\lambda$ は考えないことにしよう．

場の量子論においては場は状態ベクトルに作用する線型演算子である．
その一方でLorentz変換に対しては特定の $(j,j')$ の既約表現における「ベクトル」としてふるまう．
すなわちLorentz変換により $(j,j')$ 表現の場は

と変換する．
ここで場の添字 $A$ は既約表現の次元 $d_{j,j'}$ と等しい成分をはしるEinsteinの縮約規則を採用している．
場 $\phi_A(x)$ は $d_{j,j'}$ 次元のベクトルの「成分」であり，ベクトルそのものはLorentz変換で不変である．
そして成分の変換は一般の線型変換と仮定して $D_A{}^B(\Lambda)$ とおいた．

無限小のLorentz変換では

と展開する．
$M^{\mu\nu}$ は状態空間での表現におけるLorentz変換の生成子で $M_D^{\mu\nu}$ は場の $(j,j')$ 表現における生成子．
これらを場の変換の式へ代入して整理すれば場の交換関係として

が導かれる．
右辺第1項は座標変換による寄与であり，他方で第2項には場の成分の変換による寄与が加わっている．
$M_D^{\mu\nu}$ はLorentz変換の生成子であるから $M^{\mu\nu}$ と同じ交換関係を満たさなければならない:

ここで交換子は $[X, Y]_A{}^B=X_A{}^CY_C{}^B-Y_A{}^CX_C{}^B$ で定義される．

[スカラー場]

では固有値 $(j,j')$ を具体的に定めてLorentz変換の表現を与えよう．
まず最も簡単な $(j,j')=(0,0)$ から始める．
このとき表現空間の次元は $d_{0,0}=1$ であり，この既約表現における場は添字のない場，スカラー場 (scalar field) $\phi(x)$ が対応する:

つまりスカラー場はLorentz変換の $(0,0)$ 表現といえる．
無限小のLorentz変換ではスカラー場との交換関係

が得られる．

[左巻きスピノル場]

次に $(j,j')=(1/2,0)$ を調べよう．
次元は $d_{1/2,0}=2$ であり，対応する場は2成分量の左巻きスピノル場 (left-handed spinor field) という．
添字は $a,b,c,\cdots$ を用いて $\psi_a(x)$ と表記して

とおく．
微小なLorentz変換に対しては一次までで

と展開する．
$M_L^{\mu\nu}$ はこの既約表現における生成子である．
これをその上の式へ代入して整理すれば交換関係

が得られる．
右辺第1項はスカラー場と同じ寄与で座標変換によるものである．
他方で第2項には左巻きスピノル場の成分の変換による寄与が加わっている．

いま添字 $a,b,\cdots$ についてはスピン $1/2$ の量子力学と等価なのでPauli行列を用いて

と表現される．
ただしPauli行列は

$(J_L')_i$ に関してはスカラーと同じで場の変換による寄与がない．
このとき定義より回転とブーストの生成子はそれぞれ

と表現される．
$M_L^{ij}=\epsilon_{ijk}(S_L)_k$ かつ $M_L^{i0}=(K_L)_i$ なので

として表現される．
このときたしかにLorentz代数を満たしている．

[右巻きスピノル場]

$(j,j')=(0,1/2)$ に移ろう．
次元は左巻きスピノル場と同じく $d_{0,1/2}=2$ であり，対応する場は右巻きスピノル場 (right-handed spinor field) という．
添字はドットをつけて $\dot{a},\dot{b},\dot{c},\cdots$ を用いて $\chi_{\dot{a}}(x)$ と表記する．
右巻きスピノル場のLorentz変換を

とおく．
微小なLorentz変換に対しては一次までで

と展開する．
$M_R^{\mu\nu}$ はこの既約表現における生成子である．
これをその上の式へ代入して整理すれば交換関係

が得られる．
右辺第1項はスカラー場と同じ寄与で座標変換によるものである．
他方で第2項には右巻きスピノル場の成分の変換による寄与が加わっている．

左巻きスピノル場の（演算子に対する）Hermite共役 $(\psi_a(x))^{\dagger}$ のLorentz変換性を調べてみよう:

よってHermite共役の変換行列は複素共役をとったものであり，微小変換では

Lorentz変換の生成子の複素共役を調べると

ゆえに，

となる．
複素共役をとるとLorentz変換の生成子 $J_i,\,J_i'$ の役割が入れ替わって左巻きスピノル場の表現から右巻きスピノル場の表現へと移っている．
そこで右巻きスピノル場の表現としては

と選べば良い（ $-1$ 倍に注意せよ）．
するとLorentz変換については

左巻きスピノル場と右巻きスピノル場については

の対応関係がある．

[ベクトル場]

最後に $(j,j')=(1/2,1/2)$ を見ておこう．
このとき次元は $d_{1/2,1/2}=4$ であるから4成分のベクトル場 (vector field) が対応する．
ここでのベクトルの意味はLorentz変換に対する変換性を指してそう読んでいて数学的な一般のベクトルとは区別される．
$(1/2,1/2)$ 表現は左巻きスピノル場と右巻きスピノル場のテンソル積表現 $(1/2,0)\otimes(0,1/2)$ として理解することもできるが，後の議論に影響しないのでここでは詳細に触れない．
四元ベクトルと同様にベクトル場 $A^{\mu}(x)$ のLorentz変換は