Prerequisite
この節では自由度に見合った量を測るための数学的な手段を用意しよう.
それが座標 (coordinate) である.まず直交座標 (Cartesian coordinate) という種類の座標を導入する.
当面はこの測り方だけで問題ない.
三次元空間に導入される直交座標には目盛のついた3つのまっすぐな軸があり,それぞれ 軸
軸
軸という(区別できれば軸の名前はなんでも良い).
3軸は1点で直交しており,この直交する点 を原点 (origin) といい,測るための基準点にとる.
つまりこの点では目盛の値は3軸とも となっている.
三次元空間の適当な場所に点に対しては,3軸の目盛の値を読み取ればその点の位置は定まる.
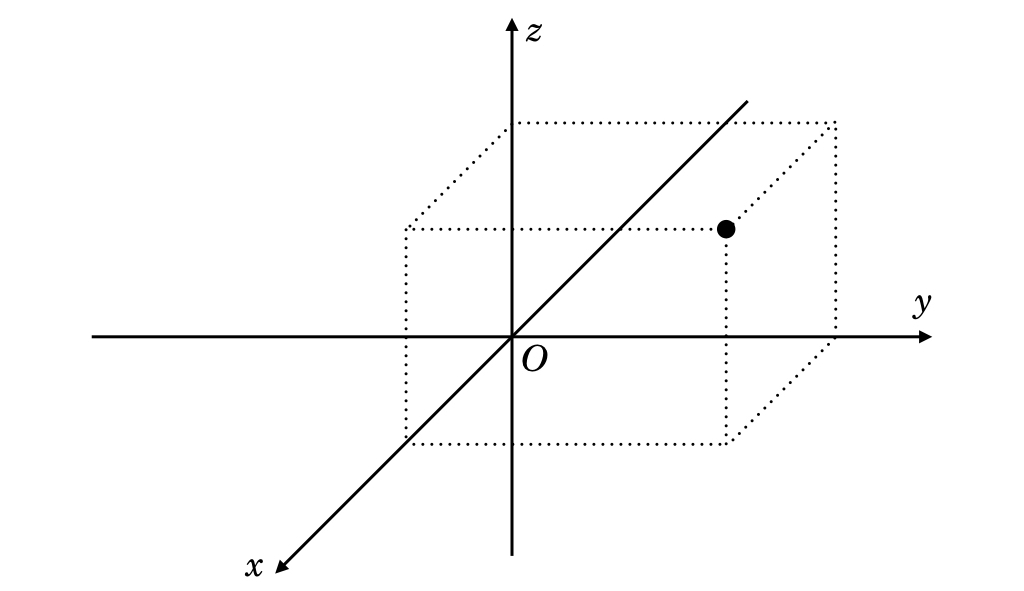
3軸から読み取られる3つの数の組を
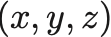
のように表記する.とくに原点はである.
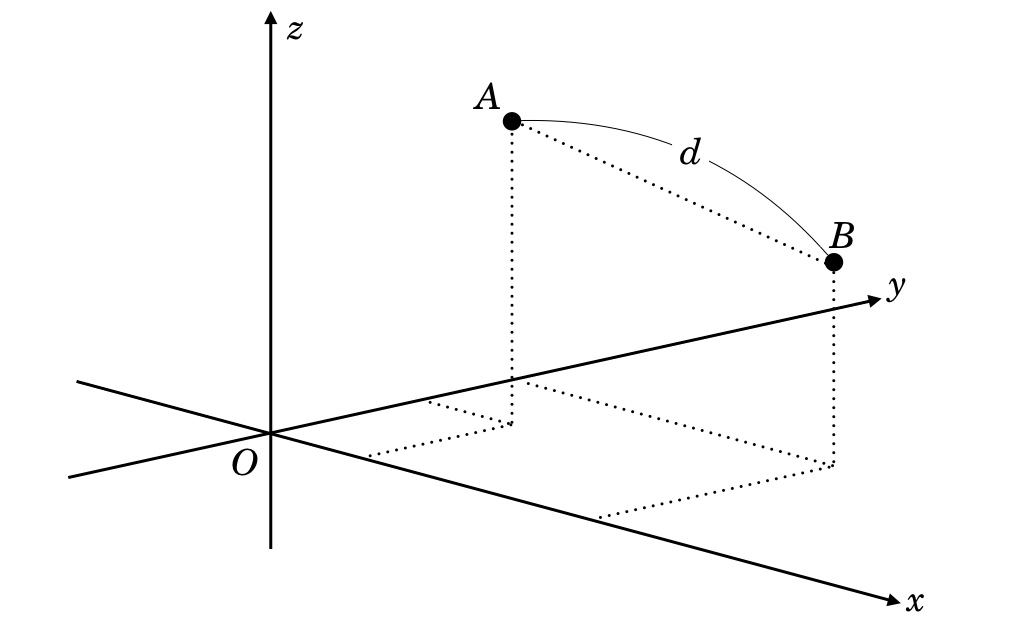
点 の座標が
,点
の座標が
であったとしよう.2点間の距離
は三平方の定理から,
距離
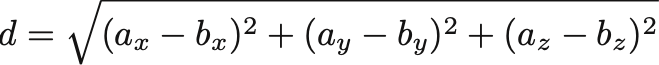
である.
物体は時間とともに動くので座標は時間の函数となる.
ある時刻 での物体の位置は
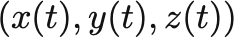
と表記する.
たとえば時刻 から
までの座標の点
の集合は1つの曲線となるだろう.
これを物体の軌道 (trajectory) という.
物理学ではふつう原点は観測する主体(人間)の位置である.
観測者と彼を原点とする座標軸と観測対象をまとめた系のことを座標系 (coordinate system) という.
座標系を一つ定めることではじめて物理の問題を考察できる.
たとえば,時速50kmで走る車に乗っている人が物の運動を観測するとしよう.
原点(観測者)は車と一緒に動くので,地面に置かれて静止している物体は(時速50kmで)動いて見える.
あるいは車と同じ向きに時速50kmで動いている物体はこの観測者からは止まって見える.
私たちが普通「動いている」と言うものは「地面に立つ観測者に対して動いている」ものということである.
が,しかしそのようなことは重要ではない.
地面はすなわち地球のことであり,地球は太陽にいる観測者に対して自転・公転している.
またその太陽も自転し銀河の中を回転運動している.
「動いている」ということは常に何かに対してであり相対的 (relative) である.
そうすると静止していることと動いていることに大きな違いはないように思える.
ある物体が静止するとは,その物体と観測者が一緒の動きをしているということであり,私たちが地面にある物が「静止している」と言っているのはそれと自分が地球と一緒に動いているということの言い換えにすぎない.
座標系を一つに決めてはじめてその系で静止している物体が何かを判断できる.
日常の中では地面が静止しているとするような座標系を無意識のうちに私たちは選んでいるのである.
座標系の例をもう少し挙げてみよう.
50m走の場合はコースに沿って軸を1本設定すれば十分である.
このコースが曲がっていても座標軸を同じように曲げれば問題なく測れる.
地球の場合は高度,水深を測るための軸が地球の中心から(1本ではあるが)放射状に伸びていなければならない.
緯度・経度を測るために必要な座標軸は分度器のような円形の軸である.
経度は 度から
度まで測れる円形の軸,緯度は
度から
度まで測れる半円形の軸が必要である.またこの二つの分度器は直交していなければならない.このように導入される座標系を球座標 (spherical coordinate) あるいは球面極座標という.
極とは中心のことである.
この座標系については円運動の節で数学的に導入することにしよう.
上記以外にも無限に多くの座標を導入することが可能である.
そして計算の都合や理論の見通しを良くするために自由に座標を設定すれば良い.
座標の導入は自然法則を記述するために人間が勝手に選んだ測り方にすぎない.
自然法則はある種の性質の良い座標ではすべて同一でなければならない.
その性質とは通常,慣性の法則とよばれるもので,これが成り立つ系では物体の静止(より正確には自由な運動)が自然に定義できるのである.
少し勇み足な注意をしておくと,自然とこの数学的概念であるところの座標系は厳密に同一のものではない.
われわれはこの2つを同一視するのであって自然の中に座標系を設定するのではない.
自然の1点を座標の中の1点に対応させることで物理学を考察するのである.
したがって座標の目盛りが等間隔であるとか真っ直ぐであるということは自然の実際ではなく,自然がそうなっていると仮定してそのような座標系に対応付けているのである.
そして実際これは正確ではなく実は自然(時空)は歪んでおり真っ直ぐではないことが多々ある.
このような時空自体の構造がどのように歪んでいるかは一般相対性理論によって議論される.
Problems
点 の座標が
と
のとき
間の距離を計算せよ.
距離の式へ代入して
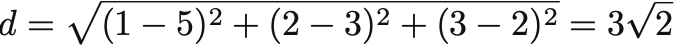
点 の距離を
と書く.このとき
が成り立つことを示せ.
距離の式の形から明らか.
点 の距離を
と書く.このとき
ならば必ず
が成り立つことを示せ.
距離の式の2乗より,
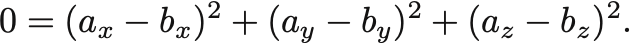
右辺の各項は必ず 以上なので等式が成立するためには

でなければならない.これはすなわち である.
逆に ならば
は明らか.
三角不等式:点 の距離を
と書く.このとき任意の点
に対して,
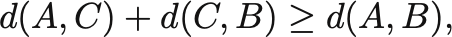
が成立することを示せ.
両辺の2乗を距離の式からそれぞれ直接計算する.
式の見通しをよくするために, とおくと,
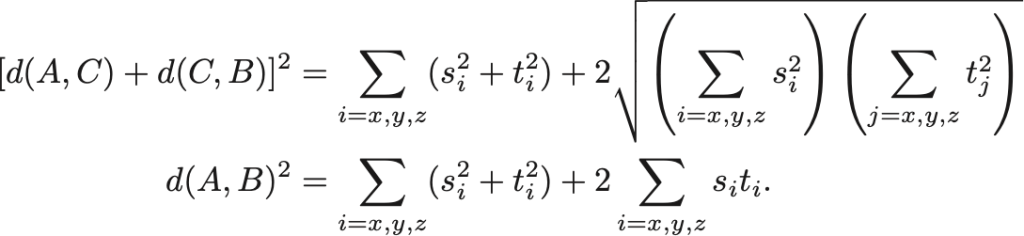
よって,
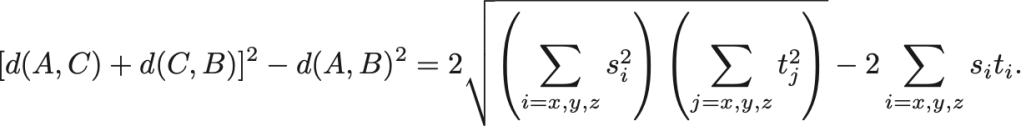
右辺はCauchy-Schwarzの不等式
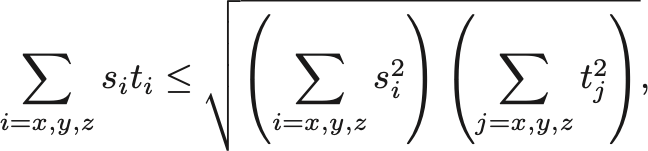
から正である.等号成立は全ての で
が等しいとき.
これは が
の通る直線上にあることと等価である.
