スカラー三重積・ベクトル三重積

2019-12-052023-03-18 ~ QuantumAtsuo

Prerequisite

位置ベクトル

この節では三次元のベクトルの二つの演算，内積と外積についての便利な記法や公式を紹介する．ベクトル $\boldsymbol{a}$ と $\boldsymbol{b}$ 内積は成分で書くと

内積

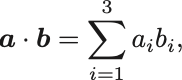
と書ける．

外積を成分で簡単に書くために次の記号を導入しよう：添字 $i,j,k$ を $1,2,3$ のいずれかとするとき

Levi-Civita記号

と定義されるこの記号をLevi-Civita記号という．Levi-Civita記号の主たる性質はその完全反対称性であり，どの2つの添字を入れ替えても符号が変わる．
2回2つの添字の入れ替えを行うと符号はもとに戻る．

Levi-Civita記号を用いると，外積の $i$ 成分がいたってシンプルにかけて，

外積

例えば第1成分についてみれば，

他の成分でも成り立っていることはたやすく確かめられる．

内積と外積の合成について考えよう．
3つのベクトル $\boldsymbol{a},\,\boldsymbol{b},\,\boldsymbol{c}$ に対して $\boldsymbol{a}\cdot(\boldsymbol{b}\times\boldsymbol{c})$ という演算をスカラー三重積という．

スカラー三重積に関して次が成り立つ：

スカラー三重積の公式

これを示すために右辺を成分記法で書き直すと，

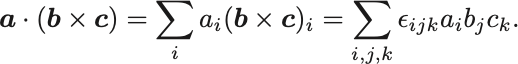
右辺で $a_i,\,b_j,\,c_k$ を順繰りに並べ替えればLevi-Civita記号の符号は変わらずに示したい残りの2つの結果を与える．たとえば，

である．

スカラー三重積の意味を幾何学的に考えてみよう．
内積の性質からベクトル $\boldsymbol{a}$ と $\boldsymbol{b}\times\boldsymbol{c}$ のなす角を $\theta$ とすると $\boldsymbol{a}\cdot(\boldsymbol{b}\times\boldsymbol{c}) = |\boldsymbol{a}||\boldsymbol{b}\times\boldsymbol{c}|\cos\theta$ ．
外積の大きさ $|\boldsymbol{b}\times\boldsymbol{c}|$ はベクトル $\boldsymbol{b}$ と $\boldsymbol{c}$ が作る平行四辺形の面積に等しい．
また $|\boldsymbol{a}|\cos\theta$ は位置ベクトル $\boldsymbol{a}$ から平行四辺形に下ろした垂線の長さに等しい．
したがってスカラー三重積 $\boldsymbol{a}\cdot(\boldsymbol{b}\times\boldsymbol{c})$ は3つのベクトルが作る平行六面体の体積に等しい．
平行六面体はどの面を底面としても同じ計算方法で体積が求まることを上の公式は示している．

スカラー三重積の幾何学的解釈

次にやはり3つのベクトル $\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$ に対して $\boldsymbol{a}\times(\boldsymbol{b}\times\boldsymbol{c})$ という演算をベクトル三重積という．

ベクトル三重積について次が成り立つ：

ベクトル三重積の公式

この証明には2つのLevi-Civita記号の積に関する次の恒等式

を用いる．

註：行列についての知識があれば右辺が次の行列式に書けることがわかるだろう：

ただし左辺に現れる記号はKroneckerのデルタとよばれ，

Kroneckerのデルタ

と定義される．Kroneckerのデルタは添字の入れ替えに対して対称で $\delta_{ij}=\delta_{ji}$ である．
2つのLevi-Civita記号の添字のうち $i$ と $a$ が同じ添字だとして和をとる（このような操作を縮約をとるという）と

$\sum\delta_{ii}=3,\,\sum\delta_{ji}\delta_{ik}=\delta_{jk}$ であることをもちいれば，

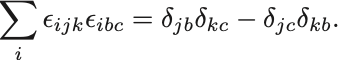
を得る．

では示したい式に戻ろう．上の結果を用いれば，

したがって所期の式を得る．

ついでに2つのLevi-Civita記号の添字のうち $i$ と $a$ ， $j$ と $b$ がそれぞれ同じとして和をとる計算をしてみよう．
同様の計算から，

さらに3つの添字がそれぞれ同じ場合は，

となる．

Problems

$\textsc{Problem1.}$

スカラー三重積とベクトル三重積の公式を成分を直接計算することによって示せ．

$\textsc{Solution.}$

（省略）

$\textsc{Problem2.}$

スカラー四重積: 次が成り立つことを示せ,

ただし $\boldsymbol{a},\,\boldsymbol{b},\,\boldsymbol{c},\,\boldsymbol{d}$ はベクトル．

$\textsc{Solution.}$

$\boldsymbol{a}\times\boldsymbol{b}$ を1つのベクトルと見てスカラー三重積の公式を適用すると，

ベクトル三重積の公式を $[\cdots]$ に用いて，

を得る．

$\textsc{Problem3. }$

Jacobi恒等式: ベクトル三重積に関して次が成り立つことを示せ,

ただし $\boldsymbol{a},\,\boldsymbol{b},\,\boldsymbol{c}$ はベクトル．

$\textsc{Solution.}$

ベクトル三重積の公式から

両辺に $0=(\boldsymbol{b}\cdot\boldsymbol{c})\boldsymbol{a}-(\boldsymbol{b}\cdot\boldsymbol{c})\boldsymbol{a}$ を加えると，

内積は対称 $\boldsymbol{a}\cdot\boldsymbol{b}=\boldsymbol{b}\cdot\boldsymbol{a}$ であることに注意すれば，

がわかる．

$\textsc{Problem4.}$

2次元のLevi-Civita記号 $\epsilon_{ij}$ を

で定義するとき次が成り立つことを示せ：

ただし $A=(a_{ij})$ は $2\times 2$ の正方行列．

$\textsc{Solution.}$

成分を直接計算すればたやすく確かめられる．

Next

速さ

“スカラー三重積・ベクトル三重積” への1件のフィードバック

ピンバック: 行列式 – 物理とはずがたり

コメントを残すコメントをキャンセル