Prerequisite
この節では具体的な対象に対してここまでの議論を適用してみよう.
マクロな系の中でも固体・液体に比べて気体は扱いやすい.
まずは気体に関する実験結果を紹介しよう.
温度一定の下で,気体の圧力を下げると体積は増大する.
すなわち気体の圧力 は体積
に反比例する:
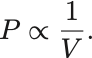
これをBoyleの法則という.
Boyleの法則は圧力が大きいとき,あるいは体積の小さいときには破綻する.
この理由については後で述べる.
ピストンのついた密封容器の中の気体を考える.等温環境の下でピストンに外力を加えて気体にかかる圧力を増大させると,Boyleの法則にしたがってピストンが押し込まれ体積が減少する.
次に圧力一定の下で,気体の温度を上げると体積は増大する.
すなわち気体の温度 は体積
に比例する:

これをCharlesの法則という.
Charlesの法則もBoyleの法則と同様に低温,あるいは体積の小さいときなどに破綻する.
Charlesの法則を用いると温度を測ることが可能になる.
比例定数を とおいて
としよう(温度の原点の定義をずらして定数項は消去した).
ある特別な温度(たとえば水の沸点) を基準に採用してそのときの体積
を計測すれば比例定数
が求まる.
このように定義された温度を理想気体温度と呼ぶ.
単位はK(ケルビン).
日常で用いられるCelcius温度( )は理想気体温度と,

という関係にある.
Cersius温度は水の融点を原点にし沸点を として定義された温度であり,理想気体温度はCersius温度と同じ目盛間隔だが原点をずらして
となるようにしたものである.
Cherlesの法則を用いた
他に有名な温度の単位にはFahrenheit温度( )があり,
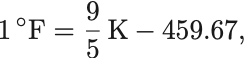
の関係で結ばれる.
Boyleの法則とCharlesの法則を合わせると,次の関係がわかる:

これはBoyle–Charlesの法則として知られる.
註)ちなみに体積一定の下で気体の温度 は圧力
に比例する:

これはGay-Lussacの法則という.
ここまでの法則は気体の量は変えていない.
温度と圧力が一定の下で,気体の量を増やすと体積が増大する.
気体の量を粒子数 で表すとすると,
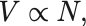
が等温・等圧環境の下で成り立つ.
これはAvogadroの法則と呼ばれる.
Boyle–Charlesの法則とAvogadroの法則を合わせると,次の関係がわかる:
理想気体の状態方程式
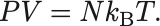
ここで はBoltzmann定数と呼ばれ,気体の種類に依存しない値を持ち,
Boltzmann定数

cf) https://physics.nist.gov/cgi-bin/cuu/Value?k
これは理想気体の状態方程式 (equation of state of ideal gas) と呼ばれる.
Boltzmann定数はマクロな系を特徴付ける定数として重要な役割を持っている.
その重要性は統計力学の章で明らかになる.
理想気体という言葉について説明を加える.
気体の分子間にはvan der Waals力と呼ばれる小さい引力が働いている.
液体はこの引力が優勢になった状態である.
一方気体では分子どうしが十分離れているならばvan der Waals力は無視できる.
あるいは分子の運動エネルギーが十分大きいときも相対的に無視できる.
このような状況はそれぞれ体積が大きいとき・温度が高いときが対応する.
そのような状況にあってvan der Waals力が無視できるような気体を理想気体と呼ぶのである.
そして理想気体のときのみ上述のBoyleの法則などが成立する.
van der Waals力が無視できなくなるとこれらの法則が破綻してしまう.
理想気体の状態方程式が破綻するような実在気体は引力の効果を加味した補正項を加えるなどして修正した状態方程式を用いる.
状態方程式は気体や液体などのマクロな対象を特徴付ける.
化学や実験物理の分野などでは粒子数は実用的ではないのでモル molを用いることが多い.
はAvogadro数でありその値は
である.
そして新たにモル気体定数 を導入する.
モルを用いた理想気体の状態方程式は
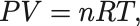
となる.本稿ではこちらは使わない.
単原子分子からなる理想気体(たとえばヘリウムやアルゴンなどの希ガス)については内部エネルギーと温度の関係が実験により知られていて
単原子分子理想気体の内部エネルギー
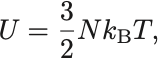
が成り立つ.
単原子分子でない,たとえば二原子分子だと前の係数が になる.
前の係数は1分子の自由度に比例していることが統計力学の議論からわかる.
ここでは事実として認めよう.
理想気体の状態方程式と内部エネルギーの式を駆使して,単原子分子理想気体の各過程についてどのようなことがいえるか議論する.
始めの平衡状態を ,後の平衡状態を
と表記する.
また全て準静的過程とする.
[定積過程: 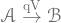 ]
]
このとき気体に加えられる仕事はない; .
内部エネルギーの変化は で与えられ,熱力学第一法則より熱は
で求まる.
[定圧過程: 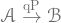 ]
]
このときも内部エネルギーの変化は と与えられる.
2つの状態方程式 と
から
と表される.
仕事は と計算され,熱力学第一法則より熱は
と求まる.
[等温過程: ]
等温過程では なので内部エネルギーの変化はない
.
仕事は状態方程式より
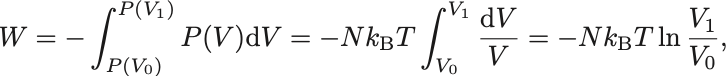
と計算され,熱力学第一法則より熱は で求まる.
[断熱過程: ]
断熱なので .断熱過程では便利な公式が知られているので,まずはそちらを導出しよう.
熱力学第一法則より .
左辺については .
右辺は .準静的過程では無限小変化
と
を定義できる.
状態方程式より .
これらを代入して整理すれば
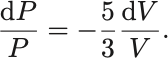
両辺を積分して整理すれば

を得る.
ここで とおいた.
つまり準静的・断熱過程の間 という量は一定となる.
これをPoissonの法則という.
状態方程式を使えば

と書ける.
Poissonの法則で定数を とおくと仕事は
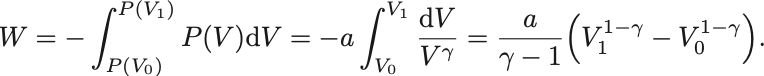
によって
を消去すれば

よってたしかに に等しいことがわかる.
