内部エネルギーと比熱

Prerequisite

熱力学第二法則

この節で系の内部エネルギー $U$ について詳しく議論しよう．
内部エネルギーは熱力学第一法則で特徴付けられていて，

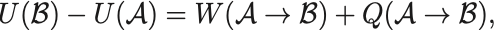
を満たし，任意の過程での系に加えられる仕事 $W$ と加えられる熱 $Q$ としたときのエネルギー保存則として解釈される．
また内部エネルギー $U$ は定義より平衡状態ごとに決まり過程に依存しない示量的な熱力学変数である．
内部エネルギーの示量性は明らかである；体積 $V$ が構成分子より十分大きければ容器の表面の効果は無視できて，内部エネルギーは体積に比例する．

断熱過程 $Q=0$ を考えると $\delta U = W$ となる．
よって系に正の仕事 $W>0$ が加えられると内部エネルギーは増加する．
仕事が準静的な体積変化で加えられるときは $W=-\int P\mathrm{d} V$ とかける．
圧力は力の大きさを面積で割ったものなので必ず $P\geq0$ であり， $W>0$ ならば $\mathrm{d} V <0$ が言える．
すなわち断熱的に系の内部エネルギーを増大させるには系を圧縮すれば良い．

孤立系が1つの仕切り壁によって2つの部分系に分離されているとする．
そして片方の部分系には温度 $T^*$ ，体積 $V^*$ の理想気体が入っていて，もう片方には温度 $T$ ，体積 $V$ の任意の物質が入っているとする．

今は $T<T^*$ と仮定しよう．
仕切り壁によって2つの部分系は何も相互作用しないとする．
仕切り板を透熱だが気体分子を通さない壁に切り替え，すぐに戻す操作を行う．
この操作によって2つの系の間で微小な熱のやりとりが起こり温度が微小変化する．
理想気体と物質の温度変化を $-\delta T^*,\,\delta T$ としよう．

この操作による過程は定積なので理想気体の内部エネルギーの変化は $\delta U = Q$ である．
理想気体の方が温度が高いので $\delta U = -(3/2)Nk_{\mathrm{B}}\delta T^*<0$ である．
一方で物質側は理想気体から正の熱 $|Q|$ を受け取る．
第一法則から $\delta U=|Q|>0$ とわかる．
したがって任意の物質についても温度が下がると内部エネルギーも下がる．

すなわち

内部エネルギー $U$ は温度 $T$ の単調非減少函数である.

といえる．
内部エネルギーの値ははじめと終わりの平衡状態における熱力学変数の値によってのみ決まり，その間の過程には依存しないので，この主張は任意の過程における任意の物質の温度変化に対しても正しい．

単調非減少性から準静的・定積過程においては，微小変化を $\mathrm{d} U = C_{\mathrm{V}}\mathrm{d} T+\mathcal{O}(\mathrm{d} T^2)$ とおくと係数 $C_{\mathrm{V}}$ は正である．
すなわち

が言える．
$C_{\mathrm{V}}$ は定積比熱または単に比熱 (specific heat) という．
定積過程では第一法則より $\delta U = Q$ ．微小変化では $Q = C_{\mathrm{V}}\mathrm{d} T$ となるので，準静的・定積過程の熱は

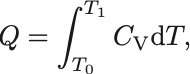
とかける．
この表式から比熱とは「一定量の物質を単位温度上げるために必要な熱量」と解釈できる．

理想気体の比熱は $C_{\mathrm{V}}=c Nk_{\mathrm{B}}$ である（単原子分子の場合 $c=3/2$ ）．
比熱の単位は $\mathrm{J\cdot K}^{-1}$ ．
化学や実験物理などでは通常，分子質量あたりの比熱

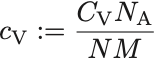
が用いられる．
ここで $N_{\mathrm{A}}\mathrm{mol}^{-1}$ はAvogadlo数， $M\mathrm{kg\cdot mol}^{-1}$ は物質のモル質量．
よって $c_{\mathrm{V}}$ の単位は $\mathrm{J\cdot kg\cdot K}^{-1}$ ．