複素数の行列表現

この節では複素数の代数構造について考察していく．
まず複素数について復習しよう．
任意の複素数 $z\in\mathbb{C}$ は一般に2つの実数 $x,\,y\in\mathbb{R}$ を用いて

と一意に表すことができる．
これは空間 $\mathbb{C}$ （複素平面という）に2次元の直交座標を導入したと解釈できる．
あるいは極座標を使えば2つの実数 $r,\,\theta\in\mathbb{R}$ を用いて，

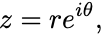
とも表せる．

複素数上の四則演算は以下のようにまとめられる: $z=x+iy,\,z'=x'+iy'$ に対して加法と乗法は

どちらの演算も可換かつ結合法則を満たす．
単位元は実数と同じく $0$ と $1$ である．
加法の逆元は任意の $z$ に対して $-z$ であり，乗法の逆元は $z\neq0$ に対して

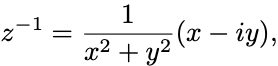
が存在する．

これは複素数の表現の1つに過ぎない．
たとえば複素平面が二次元であるなら $1$ に基本ベクトル $\boldsymbol{e}_x$ ，虚数単位 $i$ に $\boldsymbol{e}_y$ を対応させればベクトルのように

と表せる．
複素平面上の点は通常の二次元平面と同じく $(x,y)$ と表記できる．
しかしこの表現では複素数の加法は定義しやすいが乗法が定義しにくい．

そこでベクトルの線型変換として複素数を表現できないかと考える．
ベクトルの実スカラー倍は $\alpha\in\mathbb{R}$ に対して

で定義される．
これを単位行列 $\alpha I_1$ が作用しているとみることもできる．
実スカラー倍はベクトルの向きを変えずに大きさだけを変える変換である．

他方で虚数倍 $i\beta$ については複素平面上で特殊な動きをする．
複素数 $z=x+iy$ に虚数単位 $i$ をかけると $iz=-y+ix$ へ移る．
つまり複素平面上で $(x,y)$ から $(-y,x)$ へ移っている．
行列で書けば

ここに現れた行列を $J$ とおくと $i\beta$ 倍は複素平面上の点に $\beta J$ を作用しているとみることができる．
$\cos\pi/2=0,\,\sin\pi/2=1$ に気付けば $J$ は複素平面内の $\pi/2$ の回転行列でもある．
ゆえに虚スカラー倍はベクトルを $\pi/2$ だけ回転して大きさを変える変換である．

線型変換なので2種類の変換の線型和も同様に定義される．
つまり任意の複素数 $z=\alpha+i\beta$ を行列

に対応づけることができる．
この対応付けを写像 $R:\mathbb{C}\mapsto M_2(\mathbb{R})$ と表記して

とする．
単位行列は任意の行列と可換であり $J^2=-I_2$ であることから $I_2,\,J$ の演算は閉じていて複素数の演算も保っている．

また $\alpha\neq 0$ または $\beta\neq0$ であれば $\mathrm{det}\,(\alpha I_2+\beta J)\neq0$ なので逆行列

が存在し $z^{-1}$ に対応づけられる．
すると $R(1)=R(zz^{-1})=R(z^{-1}z)=I_2$ となる．

$z$ の複素共役 $z^*$ については $J$ の符号を逆転すればよいから，転置行列

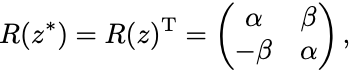
が対応する．
このときたしかに $R(zz^*)=(\alpha^2+\beta^2)I_2$ となる．

極座標表示 $z=re^{i\theta}$ では $\alpha=r\cos\theta,\,\beta=r\sin\theta$ と表せるから

となる．
$r=1$ のときは複素数 $z$ は複素平面上の単位円周上に存在する．
$R$ で表すとこれは角度 $\theta$ の二次元回転行列が対応している．
つまり円周上の点が回転という線型変換に対応することになる．

こうして複素数 $\mathbb{C}$ の代数構造を線型変換に対応づけて理解することできた．
複素数に関しては2つの実数をそのまま計算に用いる方が簡便である．
しかしもっと複雑で抽象的な代数構造を考えたい場合にこのような置き換えは非常に有用である．
特に線型変換では線型代数学の道具が使えるためこちらの方が計算が簡単になることがある．