量子力学のU(1)ゲージ理論

Prerequisite

古典電磁場中の正準量子化

古典電磁場があるときの量子力学について再考する．
Schrödinger方程式は，

座標表示をとって波動函数 $\psi(t,\boldsymbol{x})=\langle{\boldsymbol{x}|\psi,t}\rangle$ に関する方程式にすると，

となる．
この方程式は前節ではゲージ対称性を満たすような正準量子化によって導いてきた．
ただ前節では量子力学におけるゲージ対称性は後から定めたものであった．
しかし状態ベクトルのゲージ変換はそもそも確率保存則からもつべき位相の不定性を，局所的なもの（座標・時間依存性をもつもの）に拡張した変換と言える．
位相 $e^{i\theta}$ の不定性を考えるとき $\theta$ は座標・時間によらない定数である．

数学的な見地からは，とりうるすべての位相因子がなす集合とは絶対値が1の複素数全体である．
さらにこの集合は掛け算について閉じていて群構造をもつので $\mathrm{U}(1)$ 群という名前がついている：

そこで位相因子をかける変換に対応した不変性を大域的 $\mathrm{U}(1)$ 対称性 (global $\mathrm{U}(1)$ sym.)とよぶ．

他方 $\theta=\theta(t,\boldsymbol{x})$ と時間・座標依存性をもたせたものはを $\mathrm{U}(1)$ ゲージ対称性 ( $\mathrm{U}(1)$ gauge sym.)とか局所 $\mathrm{U}(1)$ 対称性とかよばれる．
$\mathrm{U}(1)$ ゲージ対称性をLorentz対称性やGalilei対称性のような基本的な対称性と思って自由Schrödinger方程式に課してみよう．
座標表示の自由Schrödinger方程式は，

形式的な議論が簡単になるように微分演算子をまとめて，

とおこう．
$\mathrm{U}(1)$ ゲージ変換，

のもとで自由Schrödinger方程式が不変であるようにしたい．

註）ここで $q$ は粒子の電荷であるが，場の量子論においては $\mathrm{U}(1)$ ゲージ対称性に付随した保存チャージ演算子に対する固有値として現れる．

しかし明らかに両辺の微分が $\theta$ に作用するため不変とはならない．
そこで大胆な解決策として微分演算子 $\hat{\mathcal{L}}$ の定義を変えて $\mathrm{U}(1)$ ゲージ変換に対して，

と変換するようにすれば変換後も方程式は成り立つ．
上の定義のままでは，

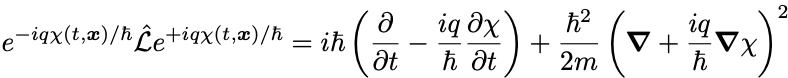
ここでの等号は演算子としてのものであることに注意せよ．
ここからわかることは微分の後ろにスカラー函数の微分が余計に現れる．
これらを自然に説明するために $\mathrm{U}(1)$ ゲージ変換に対して，

と変換するような場を新たに導入して，時間微分と座標微分を，

で定義する．
$\phi,\,\boldsymbol{A}$ を $\mathrm{U}(1)$ 対称性から導かれた $\mathrm{U}(1)$ ゲージ場という．
微分演算子の定義を変更して，

とする．この変更によって $\mathrm{U}(1)$ ゲージ対称性をもつSchrödinger方程式とは，

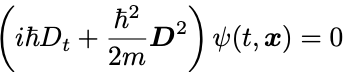
となる．
微分演算子 $D_t,\,\boldsymbol{D}$ は共変微分 (covarient derivative) とよばれる．
微分を共変微分に置き換えた方程式は古典電磁場のあるSchrödinger方程式に一致している！

共変微分のゲージ変換性は，

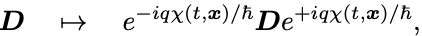
であることが定義から確かめられる．
逆にこの変換をするとき $\mathrm{U}(1)$ ゲージ場 $\phi,\boldsymbol{A}$ の変換性が定まり，Schrödinger方程式は不変となる．

共変微分の交換子を調べてみよう．
まず $D_t$ どうしは可換であり， $\boldsymbol{D}$ の成分どうしでは，

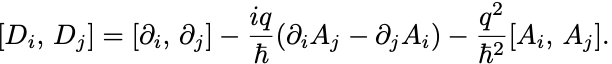
微分の可換性より第1項はおちる．
ゲージ場が古典的なスカラー函数であるので交換して第3項も落ちる．
第2項については一般に可換ではない．
第2項の微分は $\boldsymbol{A}$ のみをたたいていて後ろに来るべき波動函数には作用しない．
波動函数に作用する項は計算によって自明に落ちる．
ベクトル解析の公式から第2項は $(ie/\hbar)\epsilon_{ijk}(\boldsymbol{\nabla}\times\boldsymbol{A})_k$ と書き換えられる．
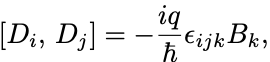
結局 $\boldsymbol{B}=\boldsymbol{\nabla}\times\boldsymbol{A}$ とおけば，

となる．
最後に $D_t$ と $\boldsymbol{D}$ では，

第1項，第3項は上と同様の理由で落ちて第2項のみが一般に残るので， $\boldsymbol{E}=-\boldsymbol{\nabla}\phi-\partial_t\boldsymbol{A}$ とおけば，

いずれにせよ共変微分の交換子は微分を含まなくなり単なる函数である．
共変微分の交換子のゲージ変換性は

であるがその計算結果は（微分演算子ではなく）単なる函数なのでゲージ不変となる．
ここで $a,b$ は $t$ または $x,y,z$ である．
よって今導入した新たな場 $\boldsymbol{B},\,\boldsymbol{E}$ がゲージ変換に対して不変であることがわかる．
この2つの場は磁場と電場に対応する場である．
こうして $\mathrm{U}(1)$ ゲージ対称性を課すことによって導入された場 $\phi,\,\boldsymbol{A}$ を古典電磁場と解釈することが可能になる．

このようなゲージ対称性に立脚した理論はゲージ理論とよばれる．
ここで展開した議論は一般のゲージ理論の基本的流れである．
$\mathrm{U}(1)$ ゲージ対称性では $\mathrm{U}(1)$ 群の元が単なる複素数であったので計算がはるかに簡単であった．
しかしながら一般のゲージ群，たとえば $\mathrm{SU}(2)$ や $\mathrm{SU}(3)$ といった群では元は行列なので複素数のようにはいかない．
特に行列の積は一般に非可換なので共変微分の交換子に場の交換子の項が付け加わる．
すると電磁場のときは現れなかった全く新しいタイプの困難に直面することになる．
$\mathrm{U}(1)$ ゲージ理論を特に可換ゲージ理論といい，後者の一般のものを非可換ゲージ理論 (nonabelian gauge theory) という．
非可換ゲージ理論については場の量子論の章で詳細に議論する．