周期的境界条件

Prerequisite

この節では定常Schrödinger方程式に対して周期的境界条件を課すことを考える．
熱力学で扱うようなマクロな系では境界からの影響は相対的に小さくなる．
現実的な系に近いのは井戸型ポテンシャルのように系の端にポテンシャルの高い壁が存在するようなモデルである．
たとえば無限に高い井戸型ポテンシャルでは境界条件として

が課せられる．
しかし非常に大きな系を考えるときには計算に便利な境界条件を課して問題を簡単化することが有効となる．

一次元の系の大きさを $2L$ （ $-L\leq x\leq +L$ ）として波動函数の周期的境界条件は

と表せる．
周期的境界条件は長さ $2L$ の円周上で定義された（なめらかな）波動函数と解釈することもできる．
この系において波動函数の規格化条件は

と課せられる．
これらの元で定常Schrödinger方程式をこれまでと同様の方法で解けば良い．

例として系にポテンシャルがない $V(x)=0$ の自由粒子を考えよう．
自由粒子のHamiltonianは $H=p^2/(2m)$ なので座標表示の定常Schrödinger方程式は

となる．
$k=\sqrt{2mE}/\hbar$ として解の形を

と仮定する．
周期的境界条件から

を満たさなければならない．
これらの条件が満たされるのは波数 $k$ が

を満たすときだけである．
よってエネルギー固有函数は

あるいは $n\in\mathbb{Z}$ に拡張して

と書ける．
エネルギー固有値は

となる．
各エネルギー固有値 $E_n$ に対して $n\neq0$ ならば $\psi_n$ と $\psi_{-n}$ の2つの異なる波動函数が存在し縮退が存在する．
$\psi_n(x)$ は運動量演算子の固有状態であり運動量の大きさは同じでも正と負の方向によって2つの状態が対応する．
そのため波動函数を実函数に選ぶこともできない．
これは周期的境界条件では $x=\pm L$ において波動函数は連続ではないことに起因している．

各固有函数に対して規格化条件を課せば定数係数 $A$ が定まって

となる．

ここで得られた固有函数と固有値に対して無限系の極限 $L\to\infty$ をとってみよう．
この極限では一次元の全空間で自由な粒子の系に一致すると期待される．
$L\to\infty$ とすれば各固有値の間隔

となって隙間がなくなっていく．
つまり運動量とエネルギーの固有値は連続に分布するようになっていく．

固有状態は座標の完全系によって

と展開される．
逆変換は運動量の完全系を用いれば

と表される．
$L\to\infty$ をとるとRiemann積分の定義から $\Delta k_n\sum_{n\in\mathbb{Z}}\to\int^{-\infty}_{-\infty}\mathrm{d} k$ に置き換えることができる．完全系の式 $\sum_{n\in\mathbb{Z}}|{n}\rangle\langle{n}|=\hat{I}$ が

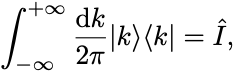
に置き換わるためには

と再規格化すればよい．
こうすると $|{x}\rangle$ は

と展開される．
これはFourier変換そのものである．
$p=\hbar k$ で変数変換すれば系の大きさが無限の場合は連続な自由粒子の運動量表示が導かれる．

最後に井戸型ポテンシャルとの対応についてコメントしておこう．
$x=\pm L$ で無限に高いポテンシャルの壁がある場合，波数（運動量）の固有値は $k_n=n\pi/(2L)$ であった．
その間隔は $\Delta k_n=\pi/(2L)$ であり，周期的境界条件の場合の半分である．
しかしラベルは正の整数 $n=1,2,3,\cdots$ のみとり，エネルギーに縮退はない．
他方で周期的境界条件の場合は $n$ は全ての整数をとり $0$ 以外は2つの縮退が存在する．
つまり前者の隣り合う2つの運動量の固有状態が後者の場合に縮退して間隔が2倍になっていると捉えることができる．
実際，系のサイズが大きい極限ではその違いがなくなる．